题目内容
已知f(x)=ax5+bx3+4,若f(-2)=3,那么f(2)的值是( )
| A、5 | B、4 | C、3 | D、-2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:构造函数F(x)=f(x)-4=ax5-bx3,根据函数的奇偶性的性质即可求解f(2).
解答:
解:∵f(x)=ax5-bx3+4,
∴f(x)-4=ax5-bx3,
构造函数F(x)=f(x)-4=ax5-bx3,
则F(-x)=f(-x)-4=-ax5+bx3=-(ax5-bx3),
即F(-x)=-F(x),
则函数F(x)=f(x)-1为奇函数,
∴F(-2)=-F(2),
即f(-2)-4=-[f(2)-4]=-f(2)+4,
∴f(2)=8-f(-2)=8-3=5,
故选:A.
∴f(x)-4=ax5-bx3,
构造函数F(x)=f(x)-4=ax5-bx3,
则F(-x)=f(-x)-4=-ax5+bx3=-(ax5-bx3),
即F(-x)=-F(x),
则函数F(x)=f(x)-1为奇函数,
∴F(-2)=-F(2),
即f(-2)-4=-[f(2)-4]=-f(2)+4,
∴f(2)=8-f(-2)=8-3=5,
故选:A.
点评:本题考查了函数的性质及其应用问题,解题时应根据函数解析式的特征,选择解题的方法,是基础题.

练习册系列答案
相关题目
函数y=
+
的定义域是( )
| 1 |
| x |
| 1 | ||
|
| A、R |
| B、(-3,+∞) |
| C、(-∞,-3) |
| D、(-3,0)∪(0,+∞) |
若sin(
-θ)=
,则cos(
+2θ)=( )
| π |
| 6 |
| 1 |
| 4 |
| 2π |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
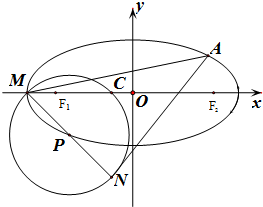 已知椭圆E的方程:
已知椭圆E的方程: