题目内容
 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA=PC,
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA=PC,(1)证明:PB⊥AC;
(2)若平面PAC⊥平面平面ABCD,∠ABC=60°,PB=AB,求二面角D-PB-C的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连接PO,AC⊥BD,且O为AC和BD的中点,由PA=PC,得AC⊥PO,从而AC⊥平面PBD,由此能证明PB⊥AC.
(Ⅱ)由已知得PO⊥平面ABCD,过点O作OH⊥PB于点H,连结CH,得CH⊥PB,从而∠OHC是二面角D-PB-C的平面角,由此能求出二面角D-PB-C的余弦值.
(Ⅱ)由已知得PO⊥平面ABCD,过点O作OH⊥PB于点H,连结CH,得CH⊥PB,从而∠OHC是二面角D-PB-C的平面角,由此能求出二面角D-PB-C的余弦值.
解答:
(Ⅰ)证明:连接PO,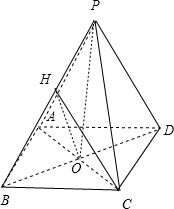
∵四边形ABCD是菱形,
∴AC⊥BD,且O为AC和BD的中点,
又PA=PC,∴AC⊥PO,
∵BD∩PO=O,BD、PO?平面PBD,
∴AC⊥平面PBD,
∵PB?平面PBD,∴PB⊥AC.
(Ⅱ)解:∵平面PAC⊥平面ABCD,
平面PAC∩平面ABCD=AC,AC⊥PO,PO?平面PAC,
∴PO⊥平面ABCD,
∵BD?平面ABCD,∴PO⊥BD,
过点O作OH⊥PB于点H,连结CH,得CH⊥PB,
∴∠OHC是二面角D-PB-C的平面角,
设PA=AB=a,
∵在菱形ABCD中,∠ABC=60°,
∴AB=BC=AC,CO=
a,BO=
a,
在Rt△POB中,PO=
=
=
a,
OH=
=
a,
∴在Rt△COH中,CH=
=
=
a,
cos∠CHO=
=
,
∴二面角D-PB-C的余弦值
.

∵四边形ABCD是菱形,
∴AC⊥BD,且O为AC和BD的中点,
又PA=PC,∴AC⊥PO,
∵BD∩PO=O,BD、PO?平面PBD,
∴AC⊥平面PBD,
∵PB?平面PBD,∴PB⊥AC.
(Ⅱ)解:∵平面PAC⊥平面ABCD,
平面PAC∩平面ABCD=AC,AC⊥PO,PO?平面PAC,
∴PO⊥平面ABCD,
∵BD?平面ABCD,∴PO⊥BD,
过点O作OH⊥PB于点H,连结CH,得CH⊥PB,
∴∠OHC是二面角D-PB-C的平面角,
设PA=AB=a,
∵在菱形ABCD中,∠ABC=60°,
∴AB=BC=AC,CO=
| 1 |
| 2 |
| ||
| 2 |
在Rt△POB中,PO=
| PB2-BO2 |
a2-
|
| 1 |
| 2 |
OH=
| PO•BO |
| PB |
| ||
| 4 |
∴在Rt△COH中,CH=
| CO2+OH2 |
(
|
| ||
| 4 |
cos∠CHO=
| OH |
| CH |
| ||
| 7 |
∴二面角D-PB-C的余弦值
| ||
| 7 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
椭圆x2+4y2=36的弦被(4,2)平分,则此弦所在直线方程为( )
| A、x-2y=0 |
| B、x+2y-8=0 |
| C、2x+3y-14=0 |
| D、x+2y-8=0 |
如果直线在平面外,那么直线与平面公共点的个数是( )
| A、1 | B、2 | C、0 | D、0或1 |
 已知函数f(x)=2sin(ωx+φ)(ω>0,-
已知函数f(x)=2sin(ωx+φ)(ω>0,- 如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF=6.
如图,四边形ABCD是正方形,DE⊥平面ABCD,AF∥DE,DE=DA=3AF=6.