题目内容
12.已知等差数列{an}的公差d≠0,其前n项和为Sn,若S9=99,且a4,a7,a12成等比数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若${T_n}=\frac{1}{S_1}+\frac{1}{S_2}+…+\frac{1}{S_n}$,证明:${T_n}<\frac{3}{4}$.
分析 (Ⅰ)由S9=99,求出a5=11,由a4,a7,a12成等比数列,求出d=2,由此能求出数列{an}的通项公式.
(Ⅱ)求出${S}_{n}=\frac{n({a}_{1}+{a}_{n})}{2}$=n(n+2),从而$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,由此利用裂项求和法能证明${T_n}<\frac{3}{4}$.
解答 解:(Ⅰ)因为等差数列{an}的公差d≠0,其前n项和为Sn,S9=99,
∴a5=11,…(2分)
由a4,a7,a12成等比数列,得${{a}_{7}}^{2}={a}_{4}{a}_{12}$,
即(11+2d)2=(11-d)(11+7d),∵d≠0,∴d=2,…(4分)
∴a1=11-4×2=3,
故an=2n+1 …(6分)
证明:(Ⅱ)${S}_{n}=\frac{n({a}_{1}+{a}_{n})}{2}$=n(n+2),$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,…(8分)
∴${T_n}=\frac{1}{S_1}+\frac{1}{S_2}+…+\frac{1}{S_n}$
=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{2}-\frac{1}{3}$)+($\frac{1}{3}-\frac{1}{4}$)+…+($\frac{1}{n-1}-\frac{1}{n+1}$)+($\frac{1}{n}-\frac{1}{n+2}$)]…(10分)
=$\frac{1}{2}$[1+$\frac{1}{2}-(\frac{1}{n+1}+\frac{1}{n+2})$]=$\frac{3}{4}-\frac{1}{2}(\frac{1}{n+1}+\frac{1}{n+2})$$<\frac{3}{4}$,
故${T_n}<\frac{3}{4}$. …(12分)
点评 本题考查数列的通项公式的求法,考查数列的前n项和小于$\frac{3}{4}$的证明,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
| A. | $2\overrightarrow{DB}+3\overrightarrow{DC}=0$ | B. | $3\overrightarrow{DB}+2\overrightarrow{DC}=0$ | C. | $\overrightarrow{OA}-5\overrightarrow{OD}=0$ | D. | $5\overrightarrow{OA}+\overrightarrow{OD}=0$ |
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | c>b>a |
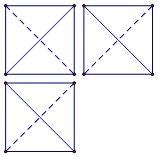
| A. | 1 | B. | 2 | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
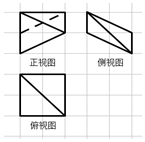 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |