题目内容
1.在(1+x)•(1+2x)5的展开式中,x4的系数为160 (用数字作答)分析 根据(1+x)•(1+2x)5的展开式中,含x4的项是第一个因式取1和x时,后一个因式应取x4和x3项,求出它们的系数和即可.
解答 解:在(1+x)•(1+2x)5的展开式中:
当第一个因式取1时,则后一个因式取含x4的项为
24${C}_{5}^{4}$•x4=80x4;
当第一个因式取x时,则后一个因式取含x3的项为
23${C}_{5}^{3}$•x3=80x3;
所以展开式中x4的系数为:80+80=160.
故答案为:160.
点评 本题考查了二项式定理的应用问题,是基础题目.

练习册系列答案
相关题目
16.执行如图所示的程序框图,则输出S=( )
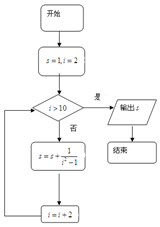

| A. | $\frac{5}{11}$ | B. | $\frac{13}{9}$ | C. | $\frac{16}{11}$ | D. | $\frac{17}{9}$ |
10.如表是某位文科生连续5次月考的历史、政治的成绩,结果如下:
(Ⅰ)求该生5次月考历史成绩的平均分和政治成绩的方差;
(Ⅱ)一般来说,学生的历史成绩与政治成绩有较强的线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{x}2}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,$\overline{x}$,$\overline{y}$表示样本均值.
| 月份 | 9 | 10 | 11 | 12 | 1 |
| 历史(x 分) | 79 | 81 | 83 | 85 | 87 |
| 政治(y 分) | 77 | 79 | 79 | 82 | 83 |
(Ⅱ)一般来说,学生的历史成绩与政治成绩有较强的线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{x}2}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,$\overline{x}$,$\overline{y}$表示样本均值.
11.已知函数$f(x)=3sin(ωx+\frac{π}{3})$的最小正周期为π,将函数f(x)的图象向右平移$\frac{π}{6}$个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是( )
| A. | g(x)为奇函数 | B. | 关于直线$x=\frac{π}{2}$对称 | ||
| C. | 关于点(π,0)对称 | D. | 在$(-\frac{π}{6},\frac{π}{4})$上递增 |