��Ŀ����
20����֪$\overrightarrow{e_1}��\overrightarrow{e_2}$�Ǽн�Ϊ60���������λ��������ʵ��k=4���ǡ�$��2\overrightarrow{e_1}-k\overrightarrow{e_2}����\overrightarrow{e_1}$���ģ�������| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ���� | ||
| C�� | ��Ҫ��������� | D�� | �Ȳ����Ҳ����Ҫ���� |
���� ������������꣬���$��2\overrightarrow{e_1}-k\overrightarrow{e_2}����\overrightarrow{e_1}$���ij�Ҫ�������жϼ��ɣ�
��� �⣺��$\overrightarrow{{e}_{1}}$=��1��0������$\overrightarrow{{e}_{2}}$=��$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$����
��$��2\overrightarrow{e_1}-k\overrightarrow{e_2}����\overrightarrow{e_1}$����
��2$\overrightarrow{{e}_{1}}$-k$\overrightarrow{{k}_{2}}$��•$\overrightarrow{{e}_{1}}$=0��
��[2��1��0��-k��$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$��]•��1��0��=2-$\frac{k}{2}$=0��
��ã�k=4��
��ʵ��k=4���ǡ�$��2\overrightarrow{e_1}-k\overrightarrow{e_2}����\overrightarrow{e_1}$���ij�Ҫ������
��ѡ��B��
���� ���⿼���˳�ֱ�Ҫ�������������������㣬��һ���е��⣮

��ϰ��ϵ�д�
�����Ŀ
10�������ijλ�Ŀ�������5���¿�����ʷ�����εijɼ���������£�
���������5���¿���ʷ�ɼ���ƽ���ֺ����γɼ��ķ��
����һ����˵��ѧ������ʷ�ɼ������γɼ��н�ǿ��������ع�ϵ�������ϱ��ṩ�����ݣ�����������x��y�����Իع鷽�̣�
�ο���ʽ��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{x}2}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$��$\overline{x}$��$\overline{y}$��ʾ������ֵ��
| �·� | 9 | 10 | 11 | 12 | 1 |
| ��ʷ��x �֣� | 79 | 81 | 83 | 85 | 87 |
| ���Σ�y �֣� | 77 | 79 | 79 | 82 | 83 |
����һ����˵��ѧ������ʷ�ɼ������γɼ��н�ǿ��������ع�ϵ�������ϱ��ṩ�����ݣ�����������x��y�����Իع鷽�̣�
�ο���ʽ��$\stackrel{��}{b}$=$\frac{\sum_{i=1}^{n}��{x}_{i}-\overline{x}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{x}_{i}-\overline{x}��^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{x}2}$��$\stackrel{��}{a}$=$\overline{y}$-$\stackrel{��}{b}$$\overline{x}$��$\overline{x}$��$\overline{y}$��ʾ������ֵ��
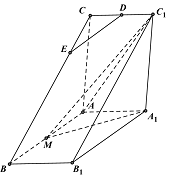 ��ͼ��ֱ������ABC-A1B1C1�У�AC��AB��AB=2AA��M��AB���е㣬��A1MC1�ǵ��������Σ�DΪCC1���е㣬EΪBC��һ�㣮
��ͼ��ֱ������ABC-A1B1C1�У�AC��AB��AB=2AA��M��AB���е㣬��A1MC1�ǵ��������Σ�DΪCC1���е㣬EΪBC��һ�㣮