题目内容

4．某三棱锥的三视图是三个边长相等的正方形及对角线，若该几何体的体积是$\frac{1}{3}$，则它的表面积是（　　）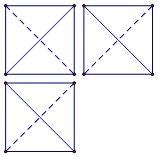
A．1B．2C．$2\sqrt{2}$D．$2\sqrt{3}$

分析 如图所示，该几何体是正方体的内接正三棱锥，求出三棱锥的棱长，利用面积公式可得几何体的表面积．

解答 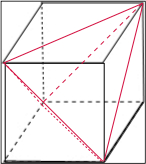解：如图所示，该几何体是正方体的内接正三棱锥．
设正方体的棱长为a，则几何体的体积是${a}^{3}-4×\frac{1}{3}×\frac{1}{2}{a}^{3}$=$\frac{1}{3}{a}^{3}$=$\frac{1}{3}$，
∴a=1，
∴三棱锥的棱长为$\sqrt{2}$，
因此此几何体的表面积S=4×$\frac{\sqrt{3}}{4}$×2=2$\sqrt{3}$，
故选：D．

点评 本题考查了正方体的内接正三棱锥表面积计算，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
14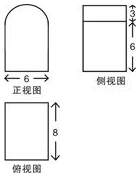．已知某几何体的三视图如图所示（正视图的弧线是半圆），根据图中标出的数据，这个几何体的表面积是（　　）
A．36π+288B．36π+216C．33π+288D．33π+216
15．已知函数f（x）=ex+ax+b（a，b∈R）在x=ln2处的切线方程为y=x-2ln2．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若k为整数，当x＞0时，（k-x）f'（x）＜x+1恒成立，求k的最大值（其中f'（x）为f（x）的导函数）．
12．已知等差数列{an}的公差d≠0，其前n项和为Sn，若S9=99，且a4，a7，a12成等比数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若${T_n}=\frac{1}{S_1}+\frac{1}{S_2}+…+\frac{1}{S_n}$，证明：${T_n}＜\frac{3}{4}$．
19．函数$f（x）=\left\{\begin{array}{l}{x^3}-3x，x≤0\\-2x+1，x＞0\end{array}\right.$，则f（x）的最大值是（　　）
A．0B．2C．1D．3
9．已知函数$f（x）=-aln（x+1）+\frac{a+1}{x+1}-a-1$（a∈R）
（1）讨论f（x）在（0，+∞）上的单调性；
（2）若对任意的正整数n都有${（1+\frac{1}{n}）^{n-a}}＞e$成立，求a的取值范围．
16．执行如图所示的程序框图，则输出S=（　　）
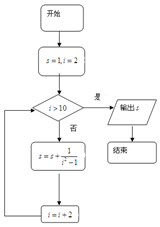
A．$\frac{5}{11}$B．$\frac{13}{9}$C．$\frac{16}{11}$D．$\frac{17}{9}$
13．在等差数列{an}中，a1=-2008，其前n项和为Sn，若$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=2，则S2008的值等于-2008．
14．已知抛物线C：y2=4x的焦点为F，过F的直线l交C于A，B两点，M为线段AB的中点，O为坐标原点．AO、BO的延长线与直线x=-4分别交于P、Q两点．
（Ⅰ）求动点M的轨迹方程；
（Ⅱ）连接OM，求△OPQ与△BOM的面积比．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网