题目内容
2.定义域为R的偶函数r(x)满足r(x+1)=r(x-1),当x∈[0,1]时,r(x)=x;函数$h(x)=\left\{\begin{array}{l}{log_3}x,x>0\\{2^x},x≤0\end{array}\right.$,则f(x)=r(x)-h(x),f(x)在[-3,4]上零点的个数为( )| A. | 4 | B. | 3 | C. | 6 | D. | 5 |
分析 根据r(x+1)=r(x-1),则r(x+2)=r[(x+1)-1]=r(x),r(x)是周期为2的偶函数,当x∈[0,1]时,r(x)=x;作出作出r(x)与h(x)的图象在[-3,4]的交点个数,即是函数f(x)在[-3,4]上零点的个数.
解答 解:由题意,满足r(x+1)=r(x-1),则r(x+2)=r[(x+1)-1]=r(x),r(x)是周期为2的函数;
当x∈[0,1]时,r(x)=x;函数$h(x)=\left\{\begin{array}{l}{log_3}x,x>0\\{2^x},x≤0\end{array}\right.$,
作出r(x)与h(x)的图象,如下: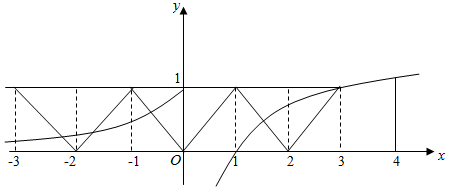
从两图象在[-3,4]交于5个点即f(x)在[-3,4]上有5个零点.
故选D.
点评 本题主要考查了函数图象与性质的运用,零点问题,图象的做法.属于中档题.

练习册系列答案
相关题目
13.在等差数列{an}中,a2=3,a5+a7=10,则a1+a10=( )
| A. | 9 | B. | 9.5 | C. | 10 | D. | 11 |
13.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线与圆${(x-\sqrt{3})^2}+{(y-1)^2}=1$相切,则此双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
17.已知函数$f(x)={x^{\frac{1}{2}}}$,则( )
| A. | ?x0∈R,使得f(x)<0 | |
| B. | ?x∈[0,+∞),f(x)≥0 | |
| C. | ?x1,x2∈[0,+∞),使得$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$ | |
| D. | ?x1∈[0,+∞),?x2∈[0,+∞)使得f(x1)>f(x2) |
14.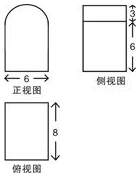 已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )
已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )
 已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )
已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )| A. | 36π+288 | B. | 36π+216 | C. | 33π+288 | D. | 33π+216 |