题目内容
17.已知$a={2^{-\frac{1}{3}}}$,$b={({2^{{{log}_2}3}})^{-\frac{1}{2}}}$,$c=\frac{1}{4}\int_0^π{sinxdx}$,则实数a,b,c的大小关系是( )| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | c>b>a |
分析 化简$a={2^{-\frac{1}{3}}}$=$\frac{1}{\root{3}{2}}$,$b={({2^{{{log}_2}3}})^{-\frac{1}{2}}}$=${3}^{-\frac{1}{2}}$=$\frac{1}{\sqrt{3}}$,$c=\frac{1}{4}\int_0^π{sinxdx}$=$\frac{1}{4}$$(-cosx){|}_{0}^{π}$=$\frac{1}{2}$,进而得出.
解答 解:∵$a={2^{-\frac{1}{3}}}$=$\frac{1}{\root{3}{2}}$,$b={({2^{{{log}_2}3}})^{-\frac{1}{2}}}$=${3}^{-\frac{1}{2}}$=$\frac{1}{\sqrt{3}}$,$c=\frac{1}{4}\int_0^π{sinxdx}$=$\frac{1}{4}$$(-cosx){|}_{0}^{π}$=$\frac{1}{2}$,
而0<$\root{3}{2}$$<\sqrt{3}$<2,
∴a>b>c.
故选:C.
点评 本题考查了函数的单调性、指数函数与对数函数的单调性、微积分基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.等比数列{an}的前n项和为Sn,已知a2a5=2a3,且a4与2a7的等差中项为$\frac{5}{4}$,则S4=( )
| A. | 29 | B. | 30 | C. | 33 | D. | 36 |
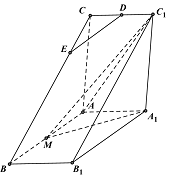 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.