题目内容
已知曲线C的极坐标方程是ρ=4cosθ.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是
(t为参数)
①把直线l与曲线C的方程化为普通方程;
②求直线l与曲线C相交所成弦的弦长.
|
①把直线l与曲线C的方程化为普通方程;
②求直线l与曲线C相交所成弦的弦长.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:①利用
可以把极坐标方程化为直角坐标方程,消去参数即可得到直线l的方程;
②利用点到直线的距离公式与弦长公式即可得出.
|
②利用点到直线的距离公式与弦长公式即可得出.
解答:
解:①.曲线C的极坐标方程ρ=4cosθ.即ρ2=4ρcosθ,化为直角坐标方程为x2+y2=4x,即(x-2)2+y2=4,可得圆心C(2,0),半径r=2.
直线l的参数方程
(t为参数),把t=
y代入x=
t+1即可得出普通方程为x-y-1=0.
②.曲线C的圆心(2,0)到直线l的距离d=
=
,
所以直线l与曲线C相交所成的弦的弦长=2
=
.
直线l的参数方程
|
| 2 |
| ||
| 2 |
②.曲线C的圆心(2,0)到直线l的距离d=
| 1 | ||
|
| ||
| 2 |
所以直线l与曲线C相交所成的弦的弦长=2
| r2-d2 |
| 14 |
点评:本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、点到直线的距离公式与弦长公式、圆的标准方程,考查了计算能力,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
已知f(x)是周期为4的奇函数,f(3)=2,则f(9)=( )
| A、6 | B、-6 | C、2 | D、-2 |
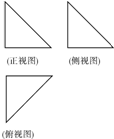 已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )
已知某三棱锥的三视图均为腰长为 2的等腰直角三角形(如图),则该棱锥的表面积为( )A、6+2
| ||
B、6+4
| ||
C、12+4
| ||
D、8+4
|
已知双曲线
-
=1的焦点为(4,0),则此双曲线的渐近线方程是( )
| x2 |
| a2 |
| y2 |
| 4 |
A、
| ||
B、x±
| ||
C、
| ||
D、x±
|
若a<b<0,则下列不等式中,一定成立的是( )
| A、a2<ab<b2 |
| B、a2>ab>b2 |
| C、a2<b2<ab |
| D、a2>b2>ab |
已知集合A={x|mx2-mx+1=0}只有一个真子集,则实数m的值为( )
| A、0 | B、4 | C、0或4 | D、0或-4 |