题目内容
已知某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:几何体为三棱锥,结合直观图判断几何体的结构特征及数据所对应的几何量,把数据代入棱锥的体积公式计算.
解答:
解:由三视图知:几何体为三棱锥S-ABC,如图:
其中SA⊥平面ABC,CO⊥平面OSA,OB=BC=AO=SA=1,
∴几何体的体积V=
×S△ABC×SA=
×
×1×1×1=
.
故选:A.

其中SA⊥平面ABC,CO⊥平面OSA,OB=BC=AO=SA=1,
∴几何体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故选:A.

点评:本题考查了由三视图求几何体的体积,解题的关键是判断几何体的结构特征及相关几何量的数据.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数f(x)=
,则函数y=f(x)-x的零点个数是( )
|
| A、0 | B、1 | C、2 | D、3 |
已知f(x)=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时,v3的值为( )
| A、27 | B、11 | C、109 | D、36 |
4名优秀学生A、B、C、D全部都被保送到甲、乙、丙3所学校,每所学校至少去一名,则不同的保送方案共有( )
| A、18种 | B、36种 |
| C、72种 | D、108种 |
设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0]时,f(x)=(
)x-1,若在区间(-2,6)内,函数y=f(x)-loga(x+2),(a>0,a≠1)恰有1个零点,则实数a的取值范围是( )
| ||
| 2 |
| A、(1,4) | ||
| B、(4,+∞) | ||
C、(
| ||
| D、(0,1)∪(1,4) |
执行如图所示的程序框图,若输出的结果为2,则输入的正整数a的可能取值的集合是( )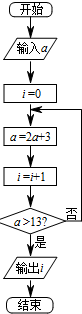

| A、{1,2,3,4,5} |
| B、{1,2,3,4,5,6} |
| C、{2,3,4,5} |
| D、{2,3,4,5,6} |
已知
=(2,1),
=(-1,k),如果
∥
,则实数k的值等于( )
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
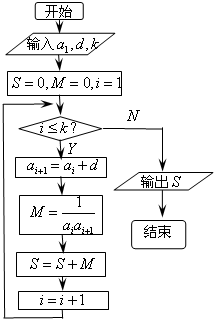 已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=
已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=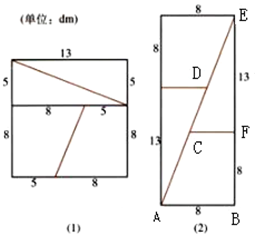 魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?
魔术大师把一块长和宽都是13dm的地毯按图(1)裁好,再按图(2)拼成矩形.计算两个图形的面积,分别得到169dm2与168dm2.魔术师得意洋洋的说,他证明了169=168.你能揭穿魔术师的奥秘吗?