题目内容

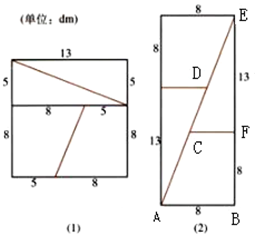魔术大师把一块长和宽都是13dm的地毯按图（1）裁好，再按图（2）拼成矩形．计算两个图形的面积，分别得到169dm2与168dm2．魔术师得意洋洋的说，他证明了169=168．你能揭穿魔术师的奥秘吗？
考点：直线的斜率
专题：直线与圆
分析：建坐标系可得kAC=
8
3
，kEC=
13
5
，kAC≠kEC，可判A、C、D、E四点不可能在同一条直线上
解答： 解：以B为坐标原点建立直角坐标系，使得BE在y轴正半轴上，AB在x轴负半轴上．
可得边AC所在直线的斜率为kAC=
8
8-5
=
8
3
，
边EC所在直线的斜率为kEC=
13
5
，即 kAC≠kEC，
∴A、C、D、E四点不可能在同一条直线上．
即图2不是矩形，魔术师的计算有误．
点评：本题考查直线的斜率，属基础题．
练习册系列答案
相关题目
已知某几何体的三视图如图所示，则该几何体的体积为（　　）
A、
1
6
B、
1
12
C、
2
3
D、
1
3
已知f（x）是R上的函数，f（xy）=f（x）+f（y），求证：f（x）是偶函数．
已知角α的终边落在直线y=
1
2
x上，求sinα+2cosα的值．
在△ABC中，A，B，C的对边分别是a，b，c，已知a=1，平面向量
m
=（sin（π-C），cosC），
n
=（sin（B+
π
2
），sinB），且
m
•
n
=sin2A．
（Ⅰ）求△ABC外接圆的面积；
（Ⅱ）已知O为△ABC的外心，由O向边BC、CA、AB引垂线，垂足分别为D、E、F，求
|
OD
|
cosA
+
|
OE
|
cosB
+
|
OF
|
cosC
的值．
已知z是复数，z-i和
z
1+i
均为实数．
（I）求复数z；
（Ⅱ）若复数（z-ti）2在复平面内对应点在第一象限，求实数t的取值范围．
在△ABC中，a，b，c分别为角A，B，C的对边，2cosA-cos2A=
3
2
；
（1）求角A的度数；
（2）若a=
3
，b+c=3，求△ABC的面积．
已知△ABC的三条边分别为a，b，c求证：
a+b
1+a+b
＞
c
1+c
．
执行如图所示的程序框图，输出的n值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网