题目内容
 如图,已知AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PA=
如图,已知AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PA=| 6 |
| 2 |
| 10 |
(1)求证:EF∥平面ABC;
(2)求证:EF⊥平面PAC;
(3)求PC与平面ABC所成角的大小.
考点:直线与平面平行的判定,直线与平面垂直的判定,直线与平面所成的角
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)由中位线定理,再由线面平行的判定定理,即可得证;
(2)先运用直径所对的角为直角,及勾股定理的逆定理,再由线面垂直的判定定理,证得BC⊥平面PAC,由于EF∥BC,即可得证;
(3)运用线面垂直的判定定理,证得PA⊥平面ABC,即∠PCA为PC与平面ABC所成角,通过解直角三角形,即可得到.
(2)先运用直径所对的角为直角,及勾股定理的逆定理,再由线面垂直的判定定理,证得BC⊥平面PAC,由于EF∥BC,即可得证;
(3)运用线面垂直的判定定理,证得PA⊥平面ABC,即∠PCA为PC与平面ABC所成角,通过解直角三角形,即可得到.
解答:
 证明:(1)在△PBC中,E是PC的中点,F是PB的中点,所以EF∥BC.
证明:(1)在△PBC中,E是PC的中点,F是PB的中点,所以EF∥BC.
又BC?平面ABC,EF?平面ABC,所以EF∥平面ABC.
(2)因为AB是⊙O的直径,所以BC⊥AC.
在Rt△ABC中,AB=2,AC=BC,所以AC=BC=
.
因为在△PCB中,PB=
,PC=2
,BC=
,
所以PB2=PC2+BC2,所以BC⊥PC.
又PC∩AC=C,所以BC⊥平面PAC.
由(1)知EF∥BC,所以EF⊥平面PAC.
(3)解:由(2)知BC⊥平面PAC,PA?平面PAC,所以PA⊥BC.
因为在△PAC中,PC=2
,PA=
,AC=
,
所以PC2=PA2+AC2,所以PA⊥AC.
又AC∩BC=C,所以PA⊥平面ABC.
所以∠PCA为PC与平面ABC所成角.
在Rt△PAC中,tan∠PAC=
=
,所以∠PCA=
,
即PC与平面ABC所成角的大小为
.
 证明:(1)在△PBC中,E是PC的中点,F是PB的中点,所以EF∥BC.
证明:(1)在△PBC中,E是PC的中点,F是PB的中点,所以EF∥BC.又BC?平面ABC,EF?平面ABC,所以EF∥平面ABC.
(2)因为AB是⊙O的直径,所以BC⊥AC.
在Rt△ABC中,AB=2,AC=BC,所以AC=BC=
| 2 |
因为在△PCB中,PB=
| 10 |
| 2 |
| 2 |
所以PB2=PC2+BC2,所以BC⊥PC.
又PC∩AC=C,所以BC⊥平面PAC.
由(1)知EF∥BC,所以EF⊥平面PAC.
(3)解:由(2)知BC⊥平面PAC,PA?平面PAC,所以PA⊥BC.
因为在△PAC中,PC=2
| 2 |
| 6 |
| 2 |
所以PC2=PA2+AC2,所以PA⊥AC.
又AC∩BC=C,所以PA⊥平面ABC.
所以∠PCA为PC与平面ABC所成角.
在Rt△PAC中,tan∠PAC=
| PA |
| AC |
| 3 |
| π |
| 3 |
即PC与平面ABC所成角的大小为
| π |
| 3 |
点评:本题考查空间直线与平面的位置关系:平行和垂直,考查线面平行的判定和线面垂直的判定和性质及运用,考查空间直线和平面所成的角的求法,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
根据工作需要,现从4名女医生,a名男医生中选3名医生组成一个救援团队,其中a=
xdx,则团队中男、女医生都有的概率为( )
| ∫ | 1 0 |
| 5 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果f(x+y)=f(x)•f(y),且f(1)=1,则
+
+…+
=( )
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(2010) |
| f(2009) |
| A、1005 | B、1006 |
| C、2008 | D、2010 |
已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax-a-x+2(a>0,且a≠1),若g(2013)=a,则f(-2013)=( )
| A、2 |
| B、2-2013-22013 |
| C、22013-2-2013 |
| D、a2 |
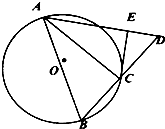 如图,AB是圆O的弦,点C在圆O上,延长BC到D,使BC=CD,AB=AD.
如图,AB是圆O的弦,点C在圆O上,延长BC到D,使BC=CD,AB=AD.