题目内容
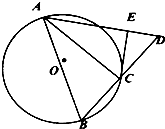如图，AB是圆O的弦，点C在圆O上，延长BC到D，使BC=CD，AB=AD．（1）求证：AB是圆O的直径；
（2）过C作圆O的切线交AD于E，且CD⊥AD，若AB=6，ED=2，求BC的长．
考点：与圆有关的比例线段
专题：
分析：（1）由BC=CD，AB=AD，得AC⊥BC，由此能求出AB是圆O的直径．
（2）由△ABC∽△CDE，得
=
，由此能求出BC=2
．
（2）由△ABC∽△CDE，得
| AB |
| CD |
| BC |
| DE |
| 3 |
解答：
（1）证明：∵BC=CD，AB=AD，
∴AC为等腰△ABD的中线，故AC⊥BC，
∴AB是圆O的直径．
（2）解：由（1）知△ABC∽△CDE，
∴
=
，
∵BC=CD，
∴BC2=AB•DE=6×2=12，
解得BC=2
．
∴AC为等腰△ABD的中线，故AC⊥BC，
∴AB是圆O的直径．
（2）解：由（1）知△ABC∽△CDE，
∴
| AB |
| CD |
| BC |
| DE |
∵BC=CD，
∴BC2=AB•DE=6×2=12，
解得BC=2
| 3 |
点评：本题考查直线是圆的直径的求法，是中档题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
相关题目
如图，已知AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PA=设函数f（x），g（x）的定义域分别为F，G，且F?G．若对任意的x∈F，都有g（x）=f（x），则称g（x）为f（x）在G上的一个“延拓函数”．已知函数f（x）=2x（x≤0），若g（x）为f（x）在R上的一个延拓函数，且g（x）是偶函数，则函数g（x）的解析式是（ ）
| A、2|x| | ||
| B、log2|x| | ||
C、（
| ||
D、log
|
已知某算法的流程图如图所示，输入的数x和y为自然数，若已知输出的有序数对为（7，6），则开始输入的有序数对（x，y）可能为（ ）| A、（14，13） |
| B、（13，14） |
| C、（11，12） |
| D、（12，11） |