题目内容
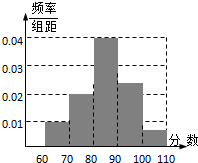为了了解某地参加计算机水平测试的1000名学生的成绩，从中随机抽取200名学生进行统计分析，分析的结果用图的频率分布直方图表示，则估计在这1000名学生中成绩小于80分的人数约有（ ）| A、100人 | B、200人 |
| C、300人 | D、400人 |
考点：频率分布直方图
专题：概率与统计
分析：由频率分布直方图先求出成绩小于80分的频率，再求这1000名学生中成绩小于80分的人数．
解答：
解：由频率分布直方图知：
成绩小于80分的频率为：（0.01+0.02）×10=0.3，
∴在这1000名学生中成绩小于80分的人数约有：
0.3×1000=300（人）．
故选：C．
成绩小于80分的频率为：（0.01+0.02）×10=0.3，
∴在这1000名学生中成绩小于80分的人数约有：
0.3×1000=300（人）．
故选：C．
点评：本题考查成绩小于80分的学生人数的求法，是基础题，解题时要注意频率分布直方图的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
已知A（1，-2），若向量
与
=（2，-3）反向，|
|=4
，则点B的坐标为（ ）
| AB |
| a |
| AB |
| 13 |
| A、（10，7） |
| B、（-10，7） |
| C、（7，-10） |
| D、（-7，10） |
六个同学平均分到甲乙两个班中，分配的种数是（ ）
| A、20 | B、40 | C、60 | D、80 |
已知函数f（x）=-x2-x+2，则函数y=f（-x）的图象是（ ）
A、 |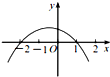
B、 |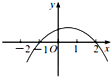
C、 |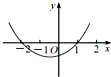
D、 |
已知蟑螂活动在如图所示的平行四边形OABC内，现有一种利用声波消灭蟑螂的机器，工作时，所发出的圆弧型声波DFE从坐标原点O向外传播，若D是DFE弧与x轴的交点，设OD=x，（0≤x≤a），圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y（图中阴影部分），则函数y=f（x）的图象大致是（ ）
已知数列{an}满足a1=2，an+1=
，则数列{an}的前63项和为（ ）
| 1+an |
| 1-an |
A、-
| ||
| B、-19 | ||
C、-
| ||
D、-
|