题目内容
六个同学平均分到甲乙两个班中，分配的种数是（ ）
| A、20 | B、40 | C、60 | D、80 |
考点：排列、组合及简单计数问题
专题：排列组合
分析：从六个同学中任选3人放到甲班，剩余的3人放到乙班即可，由排列组合的知识易得答案．
解答：
解：从六个同学中任选3人放到甲班，剩余的3人放到乙班即可，
由分步计数原理可得总的方法种数为
•
=20
故选：A
由分步计数原理可得总的方法种数为
| C | 3 6 |
| C | 3 3 |
故选：A
点评：本题考查简单的排列组合问题，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知A、B、C为空间三点，则经过三点（ ）
| A、能确定一个平面 |
| B、能确定无数个平面 |
| C、能确定一个或无数个平面 |
| D、能确定一个平面或不能确定平面 |
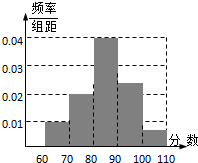为了了解某地参加计算机水平测试的1000名学生的成绩，从中随机抽取200名学生进行统计分析，分析的结果用图的频率分布直方图表示，则估计在这1000名学生中成绩小于80分的人数约有（ ）| A、100人 | B、200人 |
| C、300人 | D、400人 |
在工商管理学中，MRP指的是物质需要计划，基本MRP的体系结构如图所示．从图中能看出影响基本MRP的主要因素有（ ）个．
水以匀速注入如图容器中，试找出与容器对应的水的高度h与时间t的函数关系图象（ ）
用反证法证明命题：“若实系数一元二次方程ax2+bx+c=0（a≠0）有实数根，那么b2-4ac≥0”时，下列假设正确的是（ ）
| A、假设b2-4ac≤0 |
| B、假设b2-4ac＜0 |
| C、假设b2-4ac≥0 |
| D、假设b2-4ac＞0 |