题目内容
已知A（1，-2），若向量
与
=（2，-3）反向，|
|=4
，则点B的坐标为（ ）
| AB |
| a |
| AB |
| 13 |
| A、（10，7） |
| B、（-10，7） |
| C、（7，-10） |
| D、（-7，10） |
考点：平行向量与共线向量
专题：平面向量及应用
分析：由题设知
=k
，k＜0，所以|
|=|k|•|
|解得k=-4，由此能求出B的坐标是（-7，10）．
| AB |
| a |
| AB |
| a |
解答：
解：∵A（1，-2），向量
与
=（2，-3）反向，
∴
=k
，k＜0，
∴|
|=|k|•|
|
∴4
=|k|
=|k|•
∴|k|=4，∵k＜0，∴k=-4，
∴
=-4（2，-3）=（-8，12），
∴
=
+
=（1，-2）+（-8，12）=（-7，10）．
∴B的坐标是（-7，10）．
故选：D．
| AB |
| a |
∴
| AB |
| a |
∴|
| AB |
| a |
∴4
| 13 |
| 4+9 |
| 13 |
∴|k|=4，∵k＜0，∴k=-4，
∴
| AB |
∴
| OB |
| OA |
| AB |
∴B的坐标是（-7，10）．
故选：D．
点评：本题考查点的坐标的求法，解题时要认真审题，是基础题．
练习册系列答案
相关题目
在△ABC中，A，B，C是三角形的三内角，若sin（A-B）cosB+cos（A-B）sinB≥1，则该三角形是（ ）
| A、等腰三角形 | B、直角三角形 |
| C、正三角形 | D、不存在 |
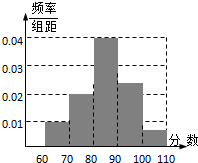为了了解某地参加计算机水平测试的1000名学生的成绩，从中随机抽取200名学生进行统计分析，分析的结果用图的频率分布直方图表示，则估计在这1000名学生中成绩小于80分的人数约有（ ）| A、100人 | B、200人 |
| C、300人 | D、400人 |
下列推理正确的是（ ）
| A、如果不买彩票，那么就不能中奖，因为你买了彩票，所以你一定中奖 | ||||||||||||||
| B、∵a＞b，a＞c，∴a-b＞a-c | ||||||||||||||
C、若a∈R+，ab＜0，则
| ||||||||||||||
D、若a，b∈R+，则lga+lgb≥2
|
已知等比数列{an}中，a1a2a3a4a5=32，且a11=8，则a7的值为（ ）
| A、4 | ||
| B、-4 | ||
| C、±4 | ||
D、±2
|