题目内容
已知抛物线D:y2=4x的焦点与椭圆Q:
+
=1(a>b>0)的右焦点F2重合,且点P(
,
)在椭圆Q上.
(Ⅰ)求椭圆Q的方程及其离心率;
(Ⅱ)若倾斜角为45°的直线l过椭圆Q的左焦点F1,且与椭圆相交于A、B两点,求△ABF2的面积.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(Ⅰ)求椭圆Q的方程及其离心率;
(Ⅱ)若倾斜角为45°的直线l过椭圆Q的左焦点F1,且与椭圆相交于A、B两点,求△ABF2的面积.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆Q的方程和离心率.
(Ⅱ)直线l的方程y=x+1,设A(x1,y1),B(x2,y2),由
,得7x2+8x-8=0,由此能求出△ABF2的面积.
|
(Ⅱ)直线l的方程y=x+1,设A(x1,y1),B(x2,y2),由
|
解答:
解:(Ⅰ)∵抛物线D:y2=4x的焦点与椭圆Q:
+
=1(a>b>0)的右焦点F2重合,
y2=4x的焦点为(1,0),
∴椭圆Q:
+
=1(a>b>0)的右焦点F2(1,0),(1分)
又点P(
,
)在椭圆Q上,
∴
,解得a2=4,b2=3,(3分)
∴椭圆Q的方程为
+
=1,(4分)
∴离心率e=
=
=
.(5分)
(Ⅱ)由(Ⅰ)知F1(-1,0),
∴直线l的方程为y-0=tan45°(x+1),(6分)
即y=x+1,设A(x1,y1),B(x2,y2),
由方程组
,
消y整理,得7x2+8x-8=0,(8分)
∴x1+x2=-
,x1x2=-
,
∴|AB|=
|x1-x2|=
=
又点F2到直线l的距离 d=
=
(10分)
∴S△ABF1=
|AB|d=
•
•
=
.(12分)
| x2 |
| a2 |
| y2 |
| b2 |
y2=4x的焦点为(1,0),
∴椭圆Q:
| x2 |
| a2 |
| y2 |
| b2 |
又点P(
| 2 |
| ||
| 2 |
∴
|
∴椭圆Q的方程为
| x2 |
| 4 |
| y2 |
| 3 |
∴离心率e=
| c |
| a |
1-
|
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)知F1(-1,0),
∴直线l的方程为y-0=tan45°(x+1),(6分)
即y=x+1,设A(x1,y1),B(x2,y2),
由方程组
|
消y整理,得7x2+8x-8=0,(8分)
∴x1+x2=-
| 8 |
| 7 |
| 8 |
| 7 |
∴|AB|=
| 2 |
| 2 |
| (x1+x2)2-4x1x2 |
| 24 |
| 7 |
又点F2到直线l的距离 d=
| |1+1| | ||
|
| 2 |
∴S△ABF1=
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 7 |
| 2 |
12
| ||
| 7 |
点评:本题考查椭圆方程及离心率的求法,考查三角形面积的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
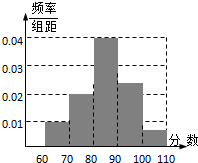 为了了解某地参加计算机水平测试的1000名学生的成绩,从中随机抽取200名学生进行统计分析,分析的结果用图的频率分布直方图表示,则估计在这1000名学生中成绩小于80分的人数约有( )
为了了解某地参加计算机水平测试的1000名学生的成绩,从中随机抽取200名学生进行统计分析,分析的结果用图的频率分布直方图表示,则估计在这1000名学生中成绩小于80分的人数约有( )| A、100人 | B、200人 |
| C、300人 | D、400人 |
在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同取法的种数是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知等比数列{an}中,a1a2a3a4a5=32,且a11=8,则a7的值为( )
| A、4 | ||
| B、-4 | ||
| C、±4 | ||
D、±2
|
用反证法证明命题:“若实系数一元二次方程ax2+bx+c=0(a≠0)有实数根,那么b2-4ac≥0”时,下列假设正确的是( )
| A、假设b2-4ac≤0 |
| B、假设b2-4ac<0 |
| C、假设b2-4ac≥0 |
| D、假设b2-4ac>0 |