题目内容
f（x）=cos2x+sinx，x∈[0，
]的值域为 ．
| π |
| 2 |
考点：二倍角的余弦,三角函数的最值
专题：三角函数的求值
分析：由条件利用二倍角的余弦公式可得f（x）=-2(sinx-
)2+
，再由sinx∈[0，1]，利用二次函数的性质求得f（x）的值域．
| 1 |
| 4 |
| 9 |
| 8 |
解答：
解：∵f（x）=cos2x+sinx=1-2sin2x+sinx=-2(sinx-
)2+
，
x∈[0，
]，∴sinx∈[0，1]，
故当sinx=
时，函数f（x）取得最大值为
；当sinx=1时，函数f（x）取得最小值为0，
故函数的值域为[0，
]，
故答案为：[0，
]．
| 1 |
| 4 |
| 9 |
| 8 |
x∈[0，
| π |
| 2 |
故当sinx=
| 1 |
| 4 |
| 9 |
| 8 |
故函数的值域为[0，
| 9 |
| 8 |
故答案为：[0，
| 9 |
| 8 |
点评：本题主要考查二倍角的余弦公式、二次函数的性质、正弦函数的定义域和值域，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
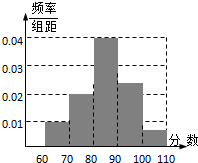为了了解某地参加计算机水平测试的1000名学生的成绩，从中随机抽取200名学生进行统计分析，分析的结果用图的频率分布直方图表示，则估计在这1000名学生中成绩小于80分的人数约有（ ）| A、100人 | B、200人 |
| C、300人 | D、400人 |