题目内容
1.函数$f(x)=\left\{{\begin{array}{l}{{{(x-1)}^2},x≥0}\\{|{{e^x}-2}|,x<0}\end{array}}\right.$则f(-1)=2-$\frac{1}{e}$,若方程f(x)=m有两个不同的实数根,则m的取值范围为(0,2).分析 根据分段函数的表达式代入求解即可,作出函数f(x)的图象,利用数形结合进行求解即可.
解答 解:由分段函数的表达式得f(-1)=|$\frac{1}{e}$-2|=2-$\frac{1}{e}$,
故答案为:2-$\frac{1}{e}$
作出函数f(x)的图象如图: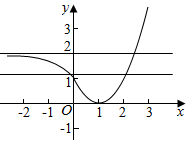
当x<0时,f(x)=2-ex∈(1,2),
∴当x≤1时,f(x)∈[0,2),
当x≥1时,f(x)≥0,
若方程f(x)=m有两个不同的实数根,
则0<m<2,
即实数m的取值范围是(0,2),
故答案为:2-$\frac{1}{e}$,(0,2).
点评 本题主要考查函数值的计算以及函数与方程的应用,利用数形结合是解决本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
9.已知函数f(x)=2cos(2x+φ)(|φ|<$\frac{π}{2}$)在区间($\frac{π}{6}$,$\frac{5π}{12}$]上单调,则2sin(φ-$\frac{π}{3}$)的取值范围是( )
| A. | (-1,1] | B. | (-$\sqrt{3}$,1] | C. | (-2,1] | D. | [-2,1] |
10.设α为第二象限,若sinα+cosα=-$\frac{\sqrt{10}}{5}$,则tan(α+$\frac{π}{4}$)等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
 已知椭圆$G:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的长轴长为$2\sqrt{2}$,离心率$e=\frac{{\sqrt{2}}}{2}$.
已知椭圆$G:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的长轴长为$2\sqrt{2}$,离心率$e=\frac{{\sqrt{2}}}{2}$.