题目内容
3.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F(2,0),点A(2,$\sqrt{2}$)为椭圆上一点.(1)求椭圆E的方程;
(2)设M、N为椭圆上两点,若直线AM的斜率与直线AN的斜率互为相反数,求证:直线MN的斜率为定值;
(3)在(2)的条件下,△AMN的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.
分析 (1)由题意可得c=2,由A满足椭圆方程,结合a,b,c的关系,可得a,b,进而得到椭圆方程;
(2)设M(x1,y1),N(x2,y2),直线AM的斜率为k,则直线AN的斜率为-k,联立直线方程和椭圆方程,运用韦达定理,结合两点的斜率公式计算即可得到所求定值;
(3)不妨设过M,N的直线方程为:$y=\frac{{\sqrt{2}}}{2}x+m$,代入椭圆方程,运用韦达定理和弦长公式,以及点到直线的距离公式,由点到直线的距离公式,结合二次函数的最值求法,即可得到所求最大值.
解答 解:(1)由已知c=2,∵$A(2,\sqrt{2})$在椭圆上,
∴$\frac{4}{a^2}+\frac{2}{b^2}=1$,
又a2=b2+c2,解得b2=4,a2=8,
可得椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1;
(2)设M(x1,y1),N(x2,y2),直线AM的斜率为k,
则直线AN的斜率为-k,
∴由$\left\{\begin{array}{l}{y-\sqrt{2}=k(x-2)}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$,消去y得(1+2k2)x2-(8k2-4$\sqrt{2}$k)x+8k2-8$\sqrt{2}$k-4=0,
由曲线E与直线l只有两个公共点,可得△>0,且x1,2是方程的二根,
∴$2{x_1}=\frac{{8{k^2}-8\sqrt{2}k-4}}{{1+2{k^2}}}$,∴${x_1}=\frac{{4{k^2}-4\sqrt{2}k-2}}{{1+2{k^2}}}$,
∴${y_1}=k({x_1}-2)+\sqrt{2}=\frac{{-2\sqrt{2}{k^2}-4k+\sqrt{2}}}{{1+2{k^2}}}$,
同理${x_2}=\frac{{4{k^2}+4\sqrt{2}k-2}}{{1+2{k^2}}}$,${y_2}=\frac{{-2\sqrt{2}{k^2}+4k+\sqrt{2}}}{{1+2{k^2}}}$
∴${k_{MN}}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{8k}{{8\sqrt{2}k}}=\frac{{\sqrt{2}}}{2}$为定值.
(3)不妨设过M,N的直线方程为:$y=\frac{{\sqrt{2}}}{2}x+m$
由$\left\{\begin{array}{l}y=\frac{{\sqrt{2}}}{2}x+m\\ \frac{x^2}{8}+\frac{y^2}{4}=1\end{array}\right.$,消去y得${x^2}+\sqrt{2}mx+{m^2}-4=0$,
由△>0,解得m2<8,${x_1}+{x_2}=-\sqrt{2}m$,${x_1}{x_2}={m^2}-4$,
计算得:$A(2,\sqrt{2})$点到直线MN的距离$d=\frac{|2m|}{{\sqrt{6}}}$,
∴${S_{△AMN}}=\frac{1}{2}•d•|MN|=\frac{1}{2}\frac{|2m|}{{\sqrt{6}}}\sqrt{1+\frac{1}{2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$
=$\frac{1}{2}•\sqrt{-2{m^4}+16{m^2}}=\frac{1}{2}\sqrt{-2{{({m^2}-4)}^2}+32}$
∴当m2=4,即m=±2时,${({S_{△AMN}})_{max}}=2\sqrt{2}$.
点评 本题考查椭圆的方程的求法,注意运用点满足椭圆方程,考查直线的斜率为定值的求法,注意运用联立直线方程和椭圆方程,运用韦达定理,以及两点的斜率公式,考查△AMN的面积是否存在最大值,运用直线和椭圆方程联立,运用韦达定理和三角形的面积公式,结合二次函数的最值的求法,属于中档题.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去.a2016等于( )
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去.a2016等于( )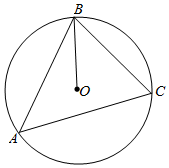 如图所示,圆O是△ABC的外接圆,BA=m,BC=$\frac{4}{m}$,∠ABC=60°,若$\overrightarrow{BO}=x\overrightarrow{BA}$+y$\overrightarrow{BC}$,则x+y的最大值是$\frac{2}{3}$.
如图所示,圆O是△ABC的外接圆,BA=m,BC=$\frac{4}{m}$,∠ABC=60°,若$\overrightarrow{BO}=x\overrightarrow{BA}$+y$\overrightarrow{BC}$,则x+y的最大值是$\frac{2}{3}$.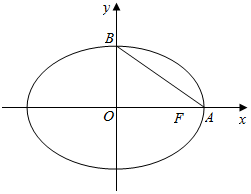 已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<2),设点A(2,0),B(0,b)与直线AB斜率相同的直线与椭圆交于M,N两点,设MN中点的轨迹为C.
已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<2),设点A(2,0),B(0,b)与直线AB斜率相同的直线与椭圆交于M,N两点,设MN中点的轨迹为C. 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$经过点 $(\frac{6}{5},\frac{4}{5})$,其离心率为$\frac{{\sqrt{3}}}{2}$,设A,B,M是椭圆C上的三点,且满足 $\overrightarrow{OM}=cosα•\overrightarrow{OA}+sinα•\overrightarrow{OB}$$(α∈(0,\frac{π}{2}))$,其