题目内容
4．已知F1，F2分别是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右两个焦点，若在双曲线C上存在点P使∠F1PF2=90°，且满足2∠PF1F2=∠PF2F1，那么双曲线C的离心率为（ ）| A． | $\sqrt{3}$+1 | B． | 2 | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{5}}{2}$ |
分析 由已知得∠F1PF2=90°，∠PF1F2=30°，∠PF2F1=60°，设|PF2|=x，则|PF1|=$\sqrt{3}x$，|F1F2|=2x，由此能求出双曲线C的离心率．
解答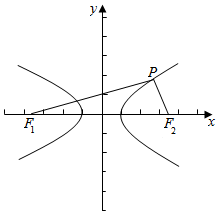 
解如图，∵∠F1PF2=90°，且满足2∠PF1F2=∠PF2F1，
∴∠F1PF2=90°，∠PF1F2=30°，∠PF2F1=60°，
设|PF2|=x，则|PF1|=$\sqrt{3}x$，|F1F2|=2x，
∴2a=$\sqrt{3}x-x$，2c=2x，
∴双曲线C的离心率e=$\frac{c}{a}=\frac{2x}{\sqrt{3}x-x}$=$\sqrt{3}+1$．
故选：A
点评 本题考查双曲线的离心率的求法，是中档题，解题时要认真审题，注意双曲线的性质的合理运用．
练习册系列答案
期末集结号系列答案
相关题目
12．已知集合A={x|x2-x-2≤0}，B={x|x2-1＞0}，则A∩B=（ ）
| A． | [-2，1） | B． | （-1，1） | C． | （1，2] | D． | （-2，-1）∪（1，2] |
17．已知函数f（x）=cos（4x-$\frac{π}{3}$）+2cos2（2x），将函数y=f（x）的图象上所有点的横坐标伸长为原来的2倍，纵坐标不变，再将所得函数图象向右平移$\frac{π}{6}$个单位，得到函数y=g（x）的图象，则函数y=g（x）的一个单调递增区间为（ ）
| A． | [-$\frac{π}{3}$，$\frac{π}{6}$] | B． | [-$\frac{π}{4}$，$\frac{π}{4}$] | C． | [$\frac{π}{6}$，$\frac{2π}{3}$] | D． | [$\frac{π}{4}$，$\frac{3π}{4}$] |
已知椭圆$G：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的长轴长为$2\sqrt{2}$，离心率$e=\frac{{\sqrt{2}}}{2}$．