题目内容
若4a=25b=10，则
+
=（ ）
| 1 |
| a |
| 1 |
| b |
| A、1 | B、2 | C、3 | D、4 |
考点：对数的运算性质
专题：函数的性质及应用
分析：由4a=25b=10，知log410=a，log2510=b，由此利用对数的运算法则能求出
+
．
| 1 |
| a |
| 1 |
| b |
解答：
解：∵4a=25b=10，
∴log410=a，log2510=b，
∴
+
=
+
=lg4+lg25
=lg（4×25）
=lg100
=2．
故选：B．
∴log410=a，log2510=b，
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| log410 |
| 1 |
| log2510 |
=lg4+lg25
=lg（4×25）
=lg100
=2．
故选：B．
点评：本题考查对数的运算法则的应用，是基础题，解题时要熟练掌握对数的性质和运算法则．
练习册系列答案
名校课堂系列答案
相关题目
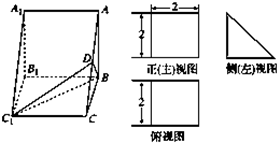直三棱柱ABC-A1B1C1的直观图及三视图如图所示，D为AC的中点，则下列命题是假命题的是（ ）| A、AB1∥平面BDC1 | ||
| B、A1C⊥平面BDC1 | ||
| C、直三棱柱的体积V=4 | ||
D、直三棱柱的外接球的表面积为4
|
设有一组圆Ck：（x-k+1）2+（y-3k）2=2k4（k∈N*）．下列四个命题，正确的有几个（ ）
①存在一条定直线与所有的圆均相切；
②存在一条定直线与所有的圆均相交；
③存在一条定直线与所有的圆均不相交；
④所有的圆均不经过原点．
①存在一条定直线与所有的圆均相切；
②存在一条定直线与所有的圆均相交；
③存在一条定直线与所有的圆均不相交；
④所有的圆均不经过原点．
| A、1 | B、2 | C、3 | D、4 |
把1010（2）化为十进制数为（ ）
| A、20 | B、12 | C、10 | D、11 |
用5种不同颜色给图中A、B、C、D四个区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，则不同的涂色方法种数为（ ）| A、120 | B、160 |
| C、180 | D、240 |
圆柱的侧面展开图是一个边长为2和4的矩形，则圆柱的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |