题目内容
把1010（2）化为十进制数为（ ）
| A、20 | B、12 | C、10 | D、11 |
考点：进位制,整除的基本性质
专题：算法和程序框图
分析：利用1010（2）=1×23+0×22+1×21+0×20即可得出．
解答：
解：1010（2）=1×23+0×22+1×21+0×20=10（10）．
故选：C．
故选：C．
点评：本题考查了把“2进制”数化为“十进制”数的方法，属于基础题．
练习册系列答案
相关题目
若4a=25b=10，则
+
=（ ）
| 1 |
| a |
| 1 |
| b |
| A、1 | B、2 | C、3 | D、4 |
函数y=sin（2x+π）是（ ）
| A、周期为π的奇函数 |
| B、周期为π的偶函数 |
| C、周期为2π的奇函数 |
| D、周期为2π的偶函数 |
若cos(π+α)=-
，则cosα的值为（ ）
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数y=3sin（2x-
）的图象是由y=3sin2x的图象经过下列哪个变换得到的（ ）
| π |
| 6 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移个
| ||
D、向左平移
|
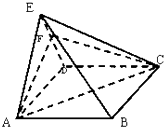如图，在四棱锥E-ABCD中，底面ABCD为边长为5的正方形，AE⊥平面CDE，AE=3．