题目内容

已知sinx+siny=
1
3
，cosx-cosy=
1
5
，则cos（x+y）的值为
 
．
考点：两角和与差的余弦函数
专题：三角函数的图像与性质
分析：将条件进行平方，然后相加，即可得到cos（x+y）的值．
解答： 解：∵sinx+siny=
1
3
，cosx-cosy=
1
5
，
∴两式平方得sin?2x+2sin?xsin?y+sin?2y=
1
9
  ①，
cos?2x-2cos?xcos?y+cos?2y=
1
25
   ②，
①+②得2+2(sin?xsin?y-cos?xcos?y)=
1
9
+
1
25
=
34
225
，
即2-2cos（x+y）=
34
225
，
即cos（x+y）=1-
17
225
=
208
225
，
故答案为：
208
225
．
点评：本题主要考查两角和的余弦公式的计算，要求熟练掌握两角和的公式，考查学生的计算能力．
练习册系列答案
相关题目
已知函数f(x)=sin(ωx+
π
6
)，(ω＞0)的周期是π．
（1）求ω和f(
π
12
)的值；
（2）求函数g(x)=f(x+
π
6
)+f(x-
π
12
)的最大值及相应x的集合．
已知命题p：?x∈R，x2-1＜0，则￢p是
 
．
直线与双曲线x2-4y2=4交于A、B两点，若线段AB的中点坐标为（8，1），则直线的方程为
 
．
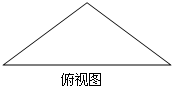一个底面是等腰直角三角形的直棱柱，侧棱长与底面三角形的腰长相等，其体积为4，它的三视图中俯视图如图所示，侧视图是一个矩形，则这个矩形的对角线长为
 
．
把89化成二进制数为
 
．
若直线（a+2）x+（1-a）y=a2（a＞0）与直线（a-1）x+（2a+3）y+2=0互相垂直，则a等于（　　）
A、1B、-1C、±1D、-2
若4a=25b=10，则
1
a
+
1
b
=（　　）
A、1B、2C、3D、4
已知圆C经过A（2，3），B（0，3）两点，且与直线x+y-5=0相切，
（1）求圆C的标准方程；
（2）在直线x+y+1=0上任取一点P，过P点作圆C的切线，切点为Q，当|PQ|最小时，求切线PQ的斜率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网