题目内容
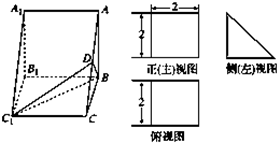 直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )
直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )| A、AB1∥平面BDC1 | ||
| B、A1C⊥平面BDC1 | ||
| C、直三棱柱的体积V=4 | ||
D、直三棱柱的外接球的表面积为4
|
考点:简单空间图形的三视图
专题:计算题,空间位置关系与距离
分析:利用面面平行的性质判断A是否正确;
根据线面垂直的判定定理证明A1C⊥平面BDC1,
利用体积公式计算棱柱的体积,可判断C是否正确;
根据正方体的外接球半径,求得外接球的体积,由此判断D是否正确.
根据线面垂直的判定定理证明A1C⊥平面BDC1,
利用体积公式计算棱柱的体积,可判断C是否正确;
根据正方体的外接球半径,求得外接球的体积,由此判断D是否正确.
解答:
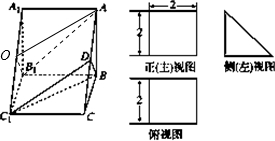 解:取A1C1中点O,连接OB1,AO,∵D为AC的中点,∴四边形DAOC1为平行四边形,
解:取A1C1中点O,连接OB1,AO,∵D为AC的中点,∴四边形DAOC1为平行四边形,
∴AO∥C1D,又四边形BDOB1为平行四边形,∴BD∥OB1,∴平面AOB1∥平面BDC1,AB1?平面AOB1,
∴AB1∥平面BDC1.
∵由三视图知A1B1⊥平面BCC1B1,BC1?平面BCC1B1,∴A1B1⊥BC1,CB1⊥BC1
∴BC1⊥平面A1B1C,∴BC1⊥A1C;
∵由侧视图知△ABC为等腰直角三角形,D为AC的中点,∴BD⊥AC,∴BD⊥平面ACC1A1,
∴A1C⊥BD,又BD∩BC1=B,
∴A1C⊥平面BDC1.故B正确;
由三视图知:直三棱柱的高为2,底面是直角边长为2的等边三角形,∴体积V=
×2×2×2=4,∴C正确;
由直三棱柱的结构特征知,直三棱柱为正方体的一半,∴外接球的半径R=
=
,
∴外接球的表面积S=4π×3=12π,∴D错误;
故选D.
 解:取A1C1中点O,连接OB1,AO,∵D为AC的中点,∴四边形DAOC1为平行四边形,
解:取A1C1中点O,连接OB1,AO,∵D为AC的中点,∴四边形DAOC1为平行四边形,∴AO∥C1D,又四边形BDOB1为平行四边形,∴BD∥OB1,∴平面AOB1∥平面BDC1,AB1?平面AOB1,
∴AB1∥平面BDC1.
∵由三视图知A1B1⊥平面BCC1B1,BC1?平面BCC1B1,∴A1B1⊥BC1,CB1⊥BC1
∴BC1⊥平面A1B1C,∴BC1⊥A1C;
∵由侧视图知△ABC为等腰直角三角形,D为AC的中点,∴BD⊥AC,∴BD⊥平面ACC1A1,
∴A1C⊥BD,又BD∩BC1=B,
∴A1C⊥平面BDC1.故B正确;
由三视图知:直三棱柱的高为2,底面是直角边长为2的等边三角形,∴体积V=
| 1 |
| 2 |
由直三棱柱的结构特征知,直三棱柱为正方体的一半,∴外接球的半径R=
| ||
| 2 |
| 3 |
∴外接球的表面积S=4π×3=12π,∴D错误;
故选D.
点评:本题考查了线面平行的判定,线面垂直的判定,考查了棱柱的体积计算及棱柱的外接球体积的求法,考查了学生的空间想象能力与运算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
若直线(a+2)x+(1-a)y=a2(a>0)与直线(a-1)x+(2a+3)y+2=0互相垂直,则a等于( )
| A、1 | B、-1 | C、±1 | D、-2 |
若4a=25b=10,则
+
=( )
| 1 |
| a |
| 1 |
| b |
| A、1 | B、2 | C、3 | D、4 |
若cos(π+α)=-
,则cosα的值为( )
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
 在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.
在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.


