题目内容
某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为( )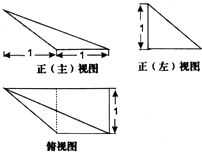

A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,分别计算侧面积,即可得出结论.
解答:
 解:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED=
解:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED=
×1×1=
,S△ABC=S△ADE=
×1×
=
,S△ACD=
×1×
=
,
故选:B.
 解:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED=
解:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 2 |
故选:B.
点评:本题考查三视图与几何体的关系,几何体的侧面积的求法,考查计算能力.

练习册系列答案
相关题目
设扇形的周长为8cm,面积为4cm2,则扇形的圆心角是( )rad.
| A、1 | B、2 | C、π | D、1或2 |
已知二次曲线
+
=1,则当m∈[-2,-1]时,该曲线的离心率e的取值范围是( )
| x2 |
| 4 |
| y2 |
| m |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
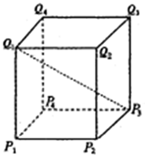 若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,集合M={x|x=
若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,集合M={x|x=