题目内容
a,b,c∈(0,
),且a=cosa,b=cos(sinb),c=sin(cosc),判断大小.
| π |
| 2 |
考点:三角函数线
专题:计算题,导数的概念及应用
分析:证明当x∈(0,
)时,sinx<x;同理可证明f(x)=sin(cosx)-x为(0,
)上的减函数,即可判断大小.
| π |
| 2 |
| π |
| 2 |
解答:
解:先证明当x∈(0,
)时,sinx<x
设y=sinx-x,则y′=cosx-1<0,∴y=sinx-x为(0,
)上的减函数,∴y<sin0-0=0,即sinx<x
同理可证明f(x)=sin(cosx)-x为(0,
)上的减函数,g(x)=cos(sinx)-x为(0,
)上的减函数
∵sina<a
∴cos(sina)-a=cos(sina)-cosa>0,而cos(sinc)-c=0,
∴g(a)>g(c),a、c∈(0,
),
∴a<c
同理∵x∈(0,
)时,sinx<x,∴sin(cosa)<cosa
∴sin(cosa)-a=sin(cosa)-cosa<0,而sin(cosb)-b=0
∴f(a)<f(b),a、b∈(0,
),
∴a>b
综上所述,b<a<c.
| π |
| 2 |
设y=sinx-x,则y′=cosx-1<0,∴y=sinx-x为(0,
| π |
| 2 |
同理可证明f(x)=sin(cosx)-x为(0,
| π |
| 2 |
| π |
| 2 |
∵sina<a
∴cos(sina)-a=cos(sina)-cosa>0,而cos(sinc)-c=0,
∴g(a)>g(c),a、c∈(0,
| π |
| 2 |
∴a<c
同理∵x∈(0,
| π |
| 2 |
∴sin(cosa)-a=sin(cosa)-cosa<0,而sin(cosb)-b=0
∴f(a)<f(b),a、b∈(0,
| π |
| 2 |
∴a>b
综上所述,b<a<c.
点评:本题考查大小比较,考查导数知识的运用,确定函数的单调性是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为( )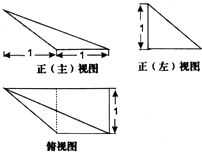

A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
已知x>0,y>0,且x+y+xy=2,则xy的最大值为( )
A、1+
| ||
B、
| ||
C、4-2
| ||
D、4+2
|
已知a=0.61.7,b=1.70.6,c=log1.70.6,则a,b,c的大小顺序是( )
| A、a<b<c |
| B、b<a<c |
| C、c>b>a |
| D、c<a<b |
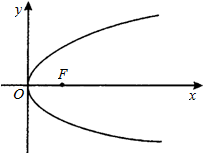 已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.
已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.