题目内容
已知二次曲线
+
=1,则当m∈[-2,-1]时,该曲线的离心率e的取值范围是( )
| x2 |
| 4 |
| y2 |
| m |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:首先判断当m∈[-2,-1]时,二次曲线为双曲线,将方程化为标准方程,求得a,b,c,再由离心率公式,即可得到范围.
解答:
解:由当m∈[-2,-1]时,二次曲线为双曲线,
双曲线
+
=1即为
-
=1,
且a2=4,b2=-m,则c2=4-m,
即有e=
=
∈[
,
],
故选C.
双曲线
| x2 |
| 4 |
| y2 |
| m |
| x2 |
| 4 |
| y2 |
| -m |
且a2=4,b2=-m,则c2=4-m,
即有e=
| c |
| a |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
故选C.
点评:本题考查双曲线的方程和性质,主要考查离心率的范围,属于基础题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
已知直线m、n、l和平面α、β,则下列命题中正确的是( )
| A、若m?α,n?α,l⊥m,l⊥n,则l⊥α |
| B、若α⊥β,m⊥β,m?α,则m∥α |
| C、若α⊥β,m?α,则m⊥β |
| D、若m?α,n?α,m∥β,n∥β,则α∥β |
某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为( )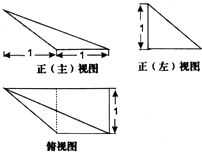

A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
过(1,2),(2,1)两点的直线的倾斜角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|