题目内容
已知曲线y=
，x=a与y=0所围成的封闭区域的面积为a3，则a= ．
| x |
考点：定积分
专题：导数的综合应用
分析：由题意利用定积分列出面积表达式，求解定积分后求得a的值．
解答：
解：由题意a3
dx=
x
=
a
，
即a
=
，解得：a=
．
故答案为：
．
| =∫ | a 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| | | a 0 |
| 2 |
| 3 |
| 3 |
| 2 |
即a
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| ||
故答案为：
| 3 |
| ||
点评：本题考查定积分的几何意义及微积分基本定理，属于基础题．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
已知cosα=-
，且α为第二象限角，那么tanα的值等于（ ）
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知直线m、n、l和平面α、β，则下列命题中正确的是（ ）
| A、若m?α，n?α，l⊥m，l⊥n，则l⊥α |
| B、若α⊥β，m⊥β，m?α，则m∥α |
| C、若α⊥β，m?α，则m⊥β |
| D、若m?α，n?α，m∥β，n∥β，则α∥β |
某几何体的三视图如图所示，则该几何体中，面积最大的侧面的面积为（ ）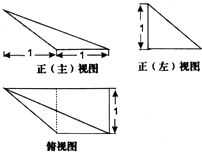
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |