题目内容
甲、乙、丙三人去完成一项任务,已知甲、乙、丙各自完成该项任务的概率分别为
,
,
,且他们是否完成任务互不影响.
(Ⅰ)求三人中只有乙完成了任务的概率;
(Ⅱ)求甲丙二人中至少有一人完成了任务的概率;
(Ⅲ)设甲、乙、丙三人中完成了任务的人数为X,求X的分布列及数学期望EX.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅰ)求三人中只有乙完成了任务的概率;
(Ⅱ)求甲丙二人中至少有一人完成了任务的概率;
(Ⅲ)设甲、乙、丙三人中完成了任务的人数为X,求X的分布列及数学期望EX.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)设事件A,B,C分别表示甲、乙、丙完成任务,则P(A)=
,P(B)=
,P(C)=
,由此能求出三人中只有乙完成了任务的概率.
(Ⅱ)甲丙二人中至少有一人完成了任务的对立事件是甲、丙二人都没有完成任务,由此利用对立事件概率计算公式能求出甲丙二人中至少有一人完成了任务的概率.
(Ⅲ)由已知得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅱ)甲丙二人中至少有一人完成了任务的对立事件是甲、丙二人都没有完成任务,由此利用对立事件概率计算公式能求出甲丙二人中至少有一人完成了任务的概率.
(Ⅲ)由已知得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答:
解:(Ⅰ)设事件A,B,C分别表示甲、乙、丙完成任务,
则P(A)=
,P(B)=
,P(C)=
,
∴三人中只有乙完成了任务的概率:
P1=P(
B
)=(1-
)×
×(1-
)=
.
(Ⅱ)甲丙二人中至少有一人完成了任务的对立事件是甲、丙二人都没有完成任务,
∴甲丙二人中至少有一人完成了任务的概率:
P2=1-[P(
)+P(
B
)]
=1-(
×
×
+
×
×
)
=1-
=
.
(Ⅲ)由已知得X的可能取值为0,1,2,3,
P(X=0)=P(
)=
×
×
=
,
P(X=1)=P(A
+
B
+
C)=
×
×
+
×
×
+
×
×
=
,
P(X=2)=P(AB
+A
C+
BC)=
×
×
+
×
×
+
×
×
=
,
P(X=3)=P(ABC)=
×
×
=
.
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=
.
则P(A)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
∴三人中只有乙完成了任务的概率:
P1=P(
. |
| A |
. |
| C |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 8 |
(Ⅱ)甲丙二人中至少有一人完成了任务的对立事件是甲、丙二人都没有完成任务,
∴甲丙二人中至少有一人完成了任务的概率:
P2=1-[P(
. |
| A |
. |
| B |
. |
| C |
. |
| A |
. |
| C |
=1-(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
=1-
| 3 |
| 8 |
=
| 5 |
| 8 |
(Ⅲ)由已知得X的可能取值为0,1,2,3,
P(X=0)=P(
. |
| A |
. |
| B |
. |
| C |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
P(X=1)=P(A
. |
| B |
. |
| C |
. |
| A |
. |
| C |
. |
| A |
. |
| B |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 11 |
| 24 |
P(X=2)=P(AB
. |
| C |
. |
| B |
. |
| A |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
P(X=3)=P(ABC)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 24 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 4 |
| 11 |
| 24 |
| 1 |
| 4 |
| 1 |
| 24 |
| 11 |
| 12 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
已知cosα=-
,且α为第二象限角,那么tanα的值等于( )
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为( )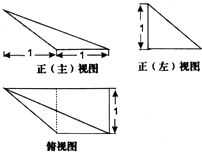

A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
已知x>0,y>0,且x+y+xy=2,则xy的最大值为( )
A、1+
| ||
B、
| ||
C、4-2
| ||
D、4+2
|
过(1,2),(2,1)两点的直线的倾斜角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a=0.61.7,b=1.70.6,c=log1.70.6,则a,b,c的大小顺序是( )
| A、a<b<c |
| B、b<a<c |
| C、c>b>a |
| D、c<a<b |