题目内容
已知角θ的顶点在坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,则
= .
| sinθ+cos(π-θ) | ||
sin(
|
考点:运用诱导公式化简求值,同角三角函数基本关系的运用
专题:三角函数的求值
分析:利用已知条件求出θ的正切函数值,通过诱导公式化简所求表达式即可求出结果.
解答:
解:∵角θ的顶点坐标原点,始边与x轴正半轴重合,终边在直线3x-y=0上,
∴可得tanθ=3.
∴则
=
=
=
=
.
故答案为:
.
∴可得tanθ=3.
∴则
| sinθ+cos(π-θ) | ||
sin(
|
| sinθ-cosθ |
| cosθ+sinθ |
| tanθ-1 |
| 1+tanθ |
| 3-1 |
| 1+3 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查诱导公式的应用,三角函数的定义,考查计算能力,属于基础题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为( )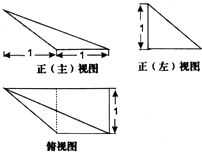

A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
已知a=0.61.7,b=1.70.6,c=log1.70.6,则a,b,c的大小顺序是( )
| A、a<b<c |
| B、b<a<c |
| C、c>b>a |
| D、c<a<b |
设M={3,5,6,8},N={4,5,7,8},则M∩N=( )
| A、{3,4,5,6,7,8} |
| B、{3,6} |
| C、{5,8} |
| D、{5,6,7,8} |
利用数学归纳法证明
+
+
+…+
<1(n∈N*,且n≥2)时,第一步不等式左端是( )
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
A、1+
| ||||||
B、
| ||||||
C、1+
| ||||||
D、
|
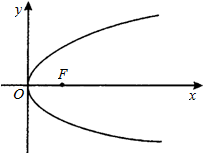 已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.
已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.