题目内容
已知G为△ABC为重心，a、b、c分别为∠A、∠B、∠C所对的边，若a
+b
+
c
=
，则∠A= ．
| GA |
| GB |
| ||
| 3 |
| GC |
| 0 |
考点：余弦定理,平面向量的基本定理及其意义
专题：解三角形
分析：G为△ABC为重心可得
+
+
=0，代入已知可得a
+b
-
c（
+
）=
，整理有（a-
c）
+（b-
c）
=
，可求a=b=
c，由余弦定理可求cosA，从而得解．
| GA |
| GB |
| GC |
| GA |
| GB |
| ||
| 3 |
| GA |
| GB |
| 0 |
| ||
| 3 |
| GA |
| ||
| 3 |
| GB |
| 0 |
| ||
| 3 |
解答：
解：因为G为△ABC为重心，所以
+
+
=0 所以，
=-(
+
)，
又因为a
+b
+
c
=
，所以：a
+b
-
c（
+
）=
，
所以（a-
c）
+（b-
c）
=
，
所以a-
c=0，b-
c=0，所以，a=b=
c，
所以，由余弦定理：cosA=
=
=
，
可得：A=
．
故答案为：
．
| GA |
| GB |
| GC |
| GC |
| GA |
| GB |
又因为a
| GA |
| GB |
| ||
| 3 |
| GC |
| 0 |
| GA |
| GB |
| ||
| 3 |
| GA |
| GB |
| 0 |
所以（a-
| ||
| 3 |
| GA |
| ||
| 3 |
| GB |
| 0 |
所以a-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
所以，由余弦定理：cosA=
| b2+c2-a2 |
| 2bc |
| ||||
2
|
| ||
| 2 |
可得：A=
| π |
| 6 |
故答案为：
| π |
| 6 |
点评：本题主要考查了平面向量的基本定理及其意义，余弦定理的简单应用，属于基本知识的考查．
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
已知cosα=-
，且α为第二象限角，那么tanα的值等于（ ）
| 4 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
下列命题中正确的是（ ）
| A、y=x3+1是奇函数 | ||
| B、y=x2，x∈[-1，2]是偶函数 | ||
C、y=
| ||
D、y=
|
某几何体的三视图如图所示，则该几何体中，面积最大的侧面的面积为（ ）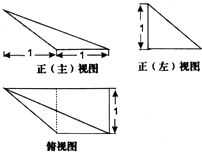
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
已知a=0.61.7，b=1.70.6，c=log1.70.6，则a，b，c的大小顺序是（ ）
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＞b＞a |
| D、c＜a＜b |