题目内容
在平面直角坐标系xOy中，已知动点P（x，y）（y≤0）到点F（0，2）的距离为d1，到x轴的距离为d2，且d1-d2=2．
（Ⅰ）求点P的轨迹E的方程；
（Ⅱ）若直线l斜率为1且过点（1，0），其与轨迹E交于点M、N，求|MN|的值．
（Ⅰ）求点P的轨迹E的方程；
（Ⅱ）若直线l斜率为1且过点（1，0），其与轨迹E交于点M、N，求|MN|的值．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）利用抛物线的定义，可求点P的轨迹E的方程；
（Ⅱ）直线l：y=x-1，联立x2=-8y（y≤0），利用韦达定理，结合弦长公式，即可求|MN|的值．
（Ⅱ）直线l：y=x-1，联立x2=-8y（y≤0），利用韦达定理，结合弦长公式，即可求|MN|的值．
解答：
解：（Ⅰ）∵动点P（x，y）（y≤0）到点F（0，2）的距离为d1，到x轴的距离为d2，且d1-d2=2，
∴由抛物线的定义可知，x2=-8y（y≤0）；
（Ⅱ）设M（x1，y1），N（x2，y2），
直线l：y=x-1，联立x2=-8y（y≤0），得x2+8x-8=0，
∴x1+x2=-8，x1x2=-8，
∴|MN|=
•
=
•
=8
，．
∴由抛物线的定义可知，x2=-8y（y≤0）；
（Ⅱ）设M（x1，y1），N（x2，y2），
直线l：y=x-1，联立x2=-8y（y≤0），得x2+8x-8=0，
∴x1+x2=-8，x1x2=-8，
∴|MN|=
| 1+k2 |
| (x1+x2)2-4x1•x2 |
| 2 |
| (-8)2-4(-8) |
| 3 |
点评：本题考查抛物线的定义域方程，考查直线与抛物线的位置关系，考查韦达定理的应用，确定抛物线的方程是关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
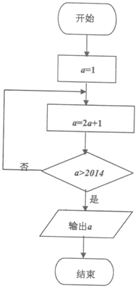根据如图所示的程序框图，变量a每次赋值后的结果依次记作：a1、a2、a3…an…．如a1=1，a2=3…．