题目内容
已知
=（cosα，sinα），
=（cosβ，sinβ）且α-β∈（-
，0），
（Ⅰ）若
•
=
，求α-β的值；
（Ⅱ）若|
-
|=
且α=
，求sinβ的值．
| a |
| b |
| π |
| 2 |
（Ⅰ）若
| a |
| b |
| ||
| 2 |
（Ⅱ）若|
| a |
| b |
| ||
| 5 |
| π |
| 3 |
考点：平面向量数量积的运算
专题：三角函数的求值,平面向量及应用
分析：（Ⅰ）由
•
=cosαcosβ+sinαsinβ=cos（α-β）=
，且α-β∈（-
，0），求出α-β的值；
（Ⅱ）由|
-
|=
，|
|=|
|=1，求出cos（α-β），sin（α-β）的值；又α=
，得出sinβ的值．
| a |
| b |
| ||
| 2 |
| π |
| 2 |
（Ⅱ）由|
| a |
| b |
| ||
| 5 |
| a |
| b |
| π |
| 3 |
解答：
解：（Ⅰ）∵
=（cosα，sinα），
=（cosβ，sinβ），
∴
•
=cosαcosβ+sinαsinβ=cos（α-β）=
；
∵α-β∈（-
，0），
∴α-β=-
；
（Ⅱ）∵|
-
|=
，|
|=|
|=1，
∴|
-
|2=2-2
•
=(
)2=
，
∴
•
=
=cos（α-β），
∴sin（α-β）=-
，
∵α=
，
∴cos（
-β）=
，sin（
-β）=-
，
∴sinβ=sin[
-（
-β）]=
×
-
×（-
）=
．
| a |
| b |
∴
| a |
| b |
| ||
| 2 |
∵α-β∈（-
| π |
| 2 |
∴α-β=-
| π |
| 6 |
（Ⅱ）∵|
| a |
| b |
| ||
| 5 |
| a |
| b |
∴|
| a |
| b |
| a |
| b |
| ||
| 5 |
| 2 |
| 5 |
∴
| a |
| b |
| 4 |
| 5 |
∴sin（α-β）=-
| 3 |
| 5 |
∵α=
| π |
| 3 |
∴cos（
| π |
| 3 |
| 4 |
| 5 |
| π |
| 3 |
| 3 |
| 5 |
∴sinβ=sin[
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
3+4
| ||
| 10 |
点评：本题考查了平面向量的应用以及三角函数求值的问题，解题时应熟练地应用平面向量的运算法则和三角函数的公式化简、求值，是综合题目．
练习册系列答案
相关题目
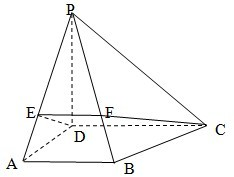已知四棱锥P-ABCD，PD⊥面ABCD，AB∥DC，AD⊥DC，AD=