题目内容
已知函数y=f（x）满足f（2x）=2x+1+1，定义数列{an}，a1=1，an+1=f（an）-1，求数列{an}的通项公式．
考点：数列的函数特性
专题：等差数列与等比数列
分析：由函数y=f（x）满足f（2x）=2x+1+1，可得f（t）=2t+1．可得f（an）=2an+1，再利用等比数列的通项公式即可得出．
解答：
解：由函数y=f（x）满足f（2x）=2x+1+1，∴f（t）=2t+1．
∵数列{an}，a1=1，an+1=f（an）-1，
∴an+1=2an+1-1，即an+1=2an．
∴数列{an}是公比为2的等比数列．
∴an=a1•2n-1=2n-1．
∴数列{an}的通项公式an=2n-1．
∵数列{an}，a1=1，an+1=f（an）-1，
∴an+1=2an+1-1，即an+1=2an．
∴数列{an}是公比为2的等比数列．
∴an=a1•2n-1=2n-1．
∴数列{an}的通项公式an=2n-1．
点评：本题考查了函数的解析式、等比数列的定义及其通项公式，属于中档题．
练习册系列答案
相关题目
用数学归纳法证明1+a+a2+…+an+1=
（a≠1，n∈N*），在验证当n=1时，等式左边应为（ ）
| 1-an+2 |
| 1-a |
| A、1 |
| B、1+a |
| C、1+a+a2 |
| D、1+a+a2+a3 |
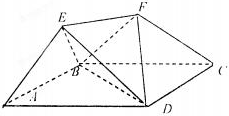如图，底面ABCD是边长为2的菱形，且∠BAD=