题目内容
3.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )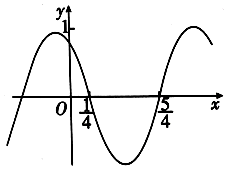
| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$),k∈Z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈Z | ||
| C. | (k-$\frac{1}{4}$,k-$\frac{3}{4}$),k∈Z | D. | (2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z |
分析 根据图象求出函数的解析式,结合三角函数的性质即可得到结论.
解答 解:从图象可以看出:图象过相邻的两个零点为($\frac{1}{4}$,0),($\frac{5}{4}$,0),
可得:T=2×$(\frac{5}{4}-\frac{1}{4})$=2,
∴ω=$\frac{2π}{2}$=π,
∴f(x)=cos(πx+φ),将点($\frac{1}{4}$,0)带入可得:cos($\frac{π}{4}$+φ)=0,
令$\frac{π}{4}$+φ=$\frac{π}{2}$,可得φ=$\frac{π}{4}$,
∴f(x)=cos(πx+$\frac{π}{4}$),
由$2kπ≤πx+\frac{π}{4}≤2kπ+π$,单点递减(k∈Z),
解得:2k-$\frac{1}{4}$≤x≤2k+$\frac{3}{4}$,k∈Z.
故选D
点评 本题主要考查三角函数单调性的求解,利用图象求出三角函数的解析式是解决本题的关键.

练习册系列答案
相关题目
1.已知命题p:?x∈(-2,2),|x-1|+|x+2|≥6,则下列叙述正确的是( )
| A. | ¬p为:?x∈(-2,2),|x-1|+|x+2|<6 | B. | ¬p为:?x∈(-2,2),|x-1|+|x+2|≥6 | ||
| C. | ¬p为:?x∈(-∞,-2]∪[2,+∞),|x-1|+|x+2|<6 | D. | ¬p为真命题 |
18.已知命题P:?x>0,总有2x>1,则¬P为( )
| A. | ?x>0,总有2x≤1 | B. | ?x≤0,总有2x≤1 | C. | ?x≤0,使得2x≤1 | D. | ?x>0,使得2x≤1 |
5.设x,y满足约束条件$\left\{\begin{array}{l}2x+y-6≤0\\ x-y-1≤0\\ x-1≥0\end{array}\right.$,若z=ax+y仅在点$({\frac{7}{3},\frac{4}{3}})$处取得最大值,则a的取值范围是( )
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
8.已知抛物线y2=2px(p>0)与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)有相同的焦点,点A是两曲线的一个公共点,若|AF|=$\frac{5p}{6}$,则椭圆的离心率为( )
| A. | $\frac{-5+\sqrt{51}}{2}$ | B. | $\frac{-5+\sqrt{61}}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{2\sqrt{2}-1}{2}$ |
13.若直线3x+y-3=0与直线6x+my+1=0平行,则它们之间的距离为( )
| A. | $\frac{{\sqrt{10}}}{4}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{7\sqrt{10}}}{10}$ | D. | $\frac{{7\sqrt{10}}}{20}$ |