题目内容
20.已知集合A={x|x2-2x-a2-2a<0},B={y|y=3x-2a,x<2}.(1)若a=3,求A∪B;
(2)若A∩B=A,求实数a的取值范围.
分析 (1)若a=3,求出A,B,即可求A∪B;
(2)若A∩B=A,A⊆B,分类讨论求实数a的取值范围.
解答 解:(1)将a=3代入A中不等式,得x2-2x-15<0,
解得-3<x<5,即A=(-3,5).
将a=3代入B中等式,得y=3x-6,
∵x≤2,∴0<3x≤9,即-6<3x-6≤3,
∴B=(-6,3],A∪B=(-6,5).
(2)∵A∩B=A,∴A⊆B,
由B中y的范围为-2a<y≤9-2a,即B=(-2a,9-2a).
由A看不等式变形,得x2-2x+1-a2-2a-1<0,
即(x-1)2-(a+1)2<0,整理得(x+a)(x-a-2)<0.
∵A∩B=A,∴A⊆B,
当a=-1时,A=∅,满足题意;
当a+2>-a,即a>-1时,A=(-a,a+2).
∵A⊆B,∴$\left\{\begin{array}{l}-2a≤-a\\ 9-2a≥a+2\end{array}\right.$
解得$0≤a≤\frac{7}{3}$; 当a+2<-a,即a>-1时,A=(a+2,-a).∴A⊆B,
∴$\left\{\begin{array}{l}-2a≤a+2\\-a≤9-2a\end{array}\right.$解得$-\frac{2}{3}≤a≤9$(舍去).
综上a=-1或$0≤a≤\frac{7}{3}$.
点评 本题考查集合的运算与关系,考查学生解不等式的能力,正确转化是关键.

练习册系列答案
相关题目
11.已知平面向量$\overrightarrow{AB}$=(1,y),$\overrightarrow{AC}$=(2,-1),且$\overrightarrow{AB}$$•\overrightarrow{AC}$=0,则3$\overrightarrow{AB}$-2$\overrightarrow{AC}$=( )
| A. | (8,1) | B. | (8,3) | C. | (-1,8) | D. | (7,8) |
15.函数f(x)=lg($\frac{2}{1-x}$+a)是奇函数,则a的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 不存在 |
5.函数f(x)=3x-$\frac{4}{x}$-a的一个零点在区间(1,2)内,则实数a的取值范围( )
| A. | (-2,7) | B. | (-1,6) | C. | (-1,7) | D. | (-2,6) |
3.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )
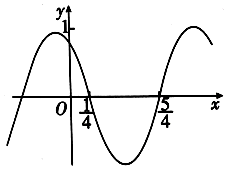

| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$),k∈Z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈Z | ||
| C. | (k-$\frac{1}{4}$,k-$\frac{3}{4}$),k∈Z | D. | (2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z |
 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.