题目内容
8.已知抛物线y2=2px(p>0)与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)有相同的焦点,点A是两曲线的一个公共点,若|AF|=$\frac{5p}{6}$,则椭圆的离心率为( )| A. | $\frac{-5+\sqrt{51}}{2}$ | B. | $\frac{-5+\sqrt{61}}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{2\sqrt{2}-1}{2}$ |
分析 求出抛物线的焦点和准线方程,即有p=2c,再由抛物线的定义求得P的坐标,代入椭圆方程,结合离心率公式和a,b,c的关系,解方程即可得到离心率.
解答 解:∵抛物线y2=2px与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)有相同的焦点F,
∴椭圆的c=$\frac{p}{2}$,即p=2c.
设A的坐标为(m,n),则由抛物线的定义可得m+$\frac{p}{2}$=$\frac{5}{6}p$,
解得m=$\frac{p}{3}$,n=±$\frac{\sqrt{6}}{3}p$,即有A($\frac{2c}{3}$,±$\frac{2\sqrt{6}}{3}c$).
代入椭圆方程可得$\frac{4{c}^{2}}{9{a}^{2}}+\frac{8{c}^{2}}{3{b}^{2}}=1$,
由离心率e=$\frac{c}{a}$,b2=c2-a2,
可得$\frac{4}{9}{e}^{2}$+$\frac{8{e}^{2}}{3(1-{e}^{2})}$=1,
即为4e4-37e2+9=0,
即有e2=9(舍去)或$\frac{1}{4}$,
解得e=$\frac{1}{2}$.
故选:C.
点评 本题考查抛物线和椭圆的定义、方程和性质,主要考查离心率的求法,运用抛物线的定义求得P的坐标是解题的关键,是中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5.函数f(x)=3x-$\frac{4}{x}$-a的一个零点在区间(1,2)内,则实数a的取值范围( )
| A. | (-2,7) | B. | (-1,6) | C. | (-1,7) | D. | (-2,6) |
3.函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )
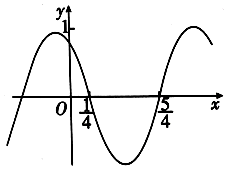

| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$),k∈Z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈Z | ||
| C. | (k-$\frac{1}{4}$,k-$\frac{3}{4}$),k∈Z | D. | (2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z |
20.将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合,若此时点C(7,3)与点D(m,n)重合,则m+n的值为( )
| A. | 6 | B. | $\frac{31}{2}$ | C. | 5 | D. | $\frac{34}{5}$ |
17.已知抛物线:y2=4x,直线l:x-y+4=0,抛物线上有一动点P到y轴的距离为d1,P到直线l的距离为d2,则d1+d2的最小值为( )
| A. | $\frac{5\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{2}}{2}$+1 | C. | $\frac{5\sqrt{2}}{2}$-2 | D. | $\frac{5\sqrt{2}}{2}$-1 |