已知定义在R上的函数f(x)存在零点.且对任意m.n∈R都满足f[$\frac{m}{2}$f]=f2=|f[f(x)]-4|+log3x-1的零点个数为3．题目和参考答案——青夏教育精英家教网—

题目内容

15．已知定义在R上的函数f（x）存在零点，且对任意m，n∈R都满足f[$\frac{m}{2}$f（m）+f（n）]=f²（m）+2n，则函数g（x）=|f[f（x）]-4|+log₃x-1的零点个数为3．

分析令f（m）=0得出f[f（n）]=2n，从而得出g（x）=|2x-4|+log₃x-1，分别作出y=1-log₃x和y=|2x-4|的函数图象，根据函数图象的交点个数判断g（x）的零点个数．

解答解：设m为f（x）的零点，则f（m）=0，
∴f[f（n）]=2n，
∴f[f（x）]=2x，
∴g（x）=|2x-4|+log₃x-1，
令g（x）=0得1-log₃x=|2x-4|，
分别作出y=1-log₃x和y=|2x-4|的函数图象，如图所示：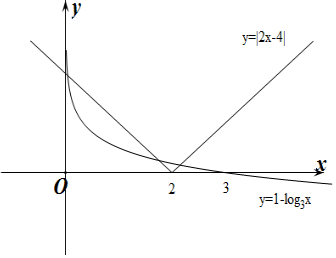

由图象可知y=1-log₃x和y=|2x-4|的函数图象有3个交点，
∴g（x）=|2x-4|+log₃x-1有3个零点．
故答案为3．

点评本题考查了函数零点与函数图象的关系，属于中档题．

练习册系列答案

13．设函数f（x）=$\left\{\begin{array}{l}{\frac{4}{x}+1，x≥4}\\{lo{g}_{2}x，0＜x＜4}\end{array}\right.$若f（a）=f（b）=c，f′（b）＜0，则a，b，c的大小关系是b＞a＞c．

3．函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（　　）

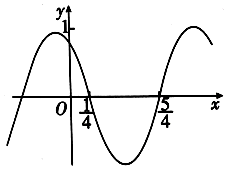
	A．	（kπ-$\frac{1}{4}$，kπ+$\frac{3}{4}$），k∈Z		B．	（2kπ-$\frac{1}{4}$，2kπ+$\frac{3}{4}$），k∈Z
	C．	（k-$\frac{1}{4}$，k-$\frac{3}{4}$），k∈Z		D．	（2k-$\frac{1}{4}$，2k+$\frac{3}{4}$），k∈Z