题目内容

1．已知命题p：?x∈（-2，2），|x-1|+|x+2|≥6，则下列叙述正确的是（　　）
A．￢p为：?x∈（-2，2），|x-1|+|x+2|＜6B．￢p为：?x∈（-2，2），|x-1|+|x+2|≥6
C．￢p为：?x∈（-∞，-2]∪[2，+∞），|x-1|+|x+2|＜6D．￢p为真命题

分析 由已知中的原命题，结合特称命题否定的定义，可得￢p．再由绝对值三角不等式，可得答案．

解答 解：∵命题p：?x∈（-2，2），|x-1|+|x+2|≥6，
∴￢p为：?x∈（-2，2），|x-1|+|x+2|＜6，
故A，B，C全错误；
根据|x-1|+|x+2|≥|（x-1）+（-x-2）|=3，
故￢p为真命题，
故D正确；
故选：D

点评 本题考查的知识点是特称命题的否定，绝对值三角不等式，难度不大，属于基础题．

练习册系列答案
相关题目
11．已知平面向量$\overrightarrow{AB}$=（1，y），$\overrightarrow{AC}$=（2，-1），且$\overrightarrow{AB}$$•\overrightarrow{AC}$=0，则3$\overrightarrow{AB}$-2$\overrightarrow{AC}$=（　　）
A．（8，1）B．（8，3）C．（-1，8）D．（7，8）
12．对于实数x，将满足“0≤y＜1且x-y为整数”的实数y称为实数x的小数部分，用符号?x＞表示．对于实数a，无穷数列{an}满足如下条件：
①a1=?a＞； ②an+1=$\left\{\begin{array}{l}{＜\frac{1}{{a}_{n}}＞（{a}_{n}≠0）}\\{0（{a}_{n}=0）}\end{array}\right.$．
（Ⅰ）若a=$\sqrt{2}$时，数列{an}通项公式为an=$\sqrt{2}$-1；
（Ⅱ）当a＞$\frac{1}{2}$时，对任意n∈N*都有an=a，则a的值为$\frac{\sqrt{5}-1}{2}$ 
9．函数f（x）=lnx的图象在点（1，0）处的切线方程是x-y-1=0．
16．已知sinα•cosα=$\frac{1}{8}$，且0＜α＜$\frac{π}{4}$，则sinα-cosα=（　　）
A．$\frac{\sqrt{3}}{2}$B．-$\frac{\sqrt{3}}{2}$C．$\frac{3}{4}$D．-17
6．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F（c，0），圆F：（x-c）2+y2=c2，直线l与双曲线C的一条渐近线垂直且在x轴上的截距为$\frac{2}{3}$a，若圆F被直线l所截得的弦长为$\frac{4\sqrt{2}}{3}$c，则双曲线的离心率为2．
13．设函数f（x）=$\left\{\begin{array}{l}{\frac{4}{x}+1，x≥4}\\{lo{g}_{2}x，0＜x＜4}\end{array}\right.$若f（a）=f（b）=c，f′（b）＜0，则a，b，c的大小关系是b＞a＞c．
3．函数f（x）=cos（ωx+φ）的部分图象如图所示，则f（x）的单调递减区间为（　　）
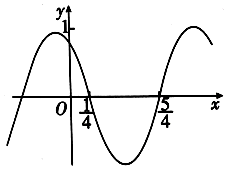
A．（kπ-$\frac{1}{4}$，kπ+$\frac{3}{4}$），k∈ZB．（2kπ-$\frac{1}{4}$，2kπ+$\frac{3}{4}$），k∈Z
C．（k-$\frac{1}{4}$，k-$\frac{3}{4}$），k∈ZD．（2k-$\frac{1}{4}$，2k+$\frac{3}{4}$），k∈Z
4．如图，在直三棱柱ABC-A1B1C1中，AA1=BC=AC=2，AB=2$\sqrt{2}$，D、E分别是的AB，BB1的中点．
（Ⅰ）证明：BC1∥平面A1CD；
（Ⅱ）求二面角D-A1C-E的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网