题目内容
12.某项竞赛分为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是$\frac{3}{4}$,$\frac{1}{2}$,$\frac{1}{4}$,且各阶段通过与否相互独立.(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为ξ,求ξ的分布列与均值.
分析 (1)记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过决赛”为事件C,则P(A)=$\frac{3}{4}$,P(B)=$\frac{1}{2}$,P(C)=$\frac{1}{4}$.那么该选手在复赛阶段被淘汰的概率P=P(A$\overline{B}$),由此能求出结果.
(2)ξ可能取值为1,2,3.分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 (本题10分)
解:(1)记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过决赛”为事件C,
则P(A)=$\frac{3}{4}$,P(B)=$\frac{1}{2}$,P(C)=$\frac{1}{4}$.
那么该选手在复赛阶段被淘汰的概率P=P(A$\overline{B}$)=P(A)P($\overline{B}$)=$\frac{3}{4}×(1-\frac{1}{2})$=$\frac{3}{8}$.…(3分)
(2)ξ可能取值为1,2,3.
P(ξ=1)=1-$\frac{3}{4}$=$\frac{1}{4}$,
P(ξ=2)=$\frac{3}{4}$×(1-$\frac{1}{2}$)=$\frac{3}{8}$,
P(ξ=3)=$\frac{3}{4}×\frac{1}{2}$=$\frac{3}{8}$.…(8分)
故ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P | $\frac{1}{4}$ | $\frac{3}{8}$ | $\frac{3}{8}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,是中档题,解题时要认真审题,注意对立事件、相互独立事件概率计算公式的合理运用.

练习册系列答案
相关题目
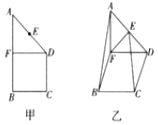 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.