题目内容
1.已知等比数列{an}的前n项和为Sn,2an+2an+2+5Sn=5Sn+1,且a1=q>1,数列{bn}满足$\frac{{b}_{n}}{{a}_{n}}$=|sin$\frac{(n+1)π}{2}$|.,若数列{bn}的前m项和为340,则m的值为8或9.分析 由2an+2an+2+5Sn=5Sn+1,可得2an+2an+2=5an+1,2+2q2=5q,且a1=q>1,解得a1=q=2.可得bn=2n•|sin$\frac{(n+1)π}{2}$|,对n分类讨论即可得出.
解答 解:由2an+2an+2+5Sn=5Sn+1,∴2an+2an+2=5an+1,∴2+2q2=5q,且a1=q>1,
解得a1=q=2.
∴an=2n.
∵数列{bn}满足$\frac{{b}_{n}}{{a}_{n}}$=|sin$\frac{(n+1)π}{2}$|.∴bn=2n•|sin$\frac{(n+1)π}{2}$|,
∴b2n-1=22n-1•|sin(nπ)|=0,b2n=22n$|sin\frac{(2n+1)π}{2}|$=22n.
∵数列{bn}的前m项和为340,假设m=2n.
∴b2+b4+…+b2n=22+24+…+22n=340,
∴$\frac{4({4}^{n}-1)}{4-1}$=340,解得n=4.
∴m=8.
∵a9=0.
∴m=9时也满足条件.
∴m=8或9.
故答案为:8或9.
点评 本题考查了等比数列的通项公式与求和公式、分类讨论方法、分组求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
11.已知全集U=R,集合A={x|x2-x-6≤0},$B=\left\{{\left.x\right|\frac{4-x}{x+1}≤0}\right\}$,那么集合A∩(∁UB)=( )
| A. | [-2,4) | B. | (-1,3] | C. | [-2,-1] | D. | [-1,3] |
13.设f(x)=$\left\{\begin{array}{l}{-x+1,0≤x≤1}\\{lnx,1<x≤e}\end{array}\right.$,直线x=0,x=e,y=0,y=1所围成的区域为M,曲线y=f(x)与直线y=1围成的区域为N,在区域M内任取一个点P,则点P在区域N内概率为( )
| A. | $\frac{2e-3}{2e}$ | B. | $\frac{3}{2e}$ | C. | $\frac{{e}^{e}{-e}^{2}+e-1}{e}$ | D. | $\frac{e-1}{e+1}$ |
10.若点P为抛物线y=2x2上的动点,F为抛物线的焦点,则|PF|的最小值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
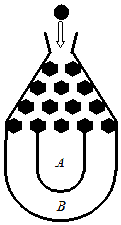 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.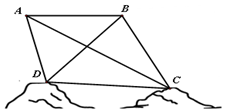 为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.
为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.