题目内容
19.已知抛物线y2=2px(p>0)的焦点F与双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且$|{AK}|=\sqrt{2}|{AF}|$,则A点的横坐标为3.分析 根据双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$得出其右焦点坐标,可知抛物线的焦点坐标,从而得到抛物线的方程和准线方程,进而可求得K的坐标,设A(x0,y0),过A点向准线作垂线AB,则B(-3,y0),根据|AK|=$\sqrt{2}$|AF|及AF=AB=x0-(-3)=x0+3,进而可求得A点坐标.
解答 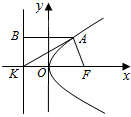 解:∵双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$,其右焦点坐标为(3,0).
解:∵双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$,其右焦点坐标为(3,0).
∴抛物线C:y2=12x,准线为x=-3,
∴K(-3,0)
设A(x0,y0),过A点向准线作垂线AB,则B(-3,y0)
∵$|{AK}|=\sqrt{2}|{AF}|$,AF=AB=x0-(-3)=x0+3,
∴由BK2=AK2-AB2得BK2=AB2,从而y02=(x0+3)2,即12x0=(x0+3)2,
解得x0=3.
故答案为:3.
点评 本题主要考查了抛物线的简单性质.考查了学生对抛物线基础知识的熟练掌握.

练习册系列答案
相关题目
15.已知cosθ-sinθ=$\frac{4}{3}$,则sinθcosθ=( )
| A. | -$\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | -$\frac{7}{18}$ | D. | $\frac{7}{18}$ |
16.函数f(x)=x2-2x-3,则f(1-x)=( )
| A. | -x2-4 | B. | x2-4 | C. | (x-1)2-4 | D. | 4-x2 |
7.已知集合A={x|x2-1=0},则下列式子表示正确的有( )
①1∈A②{-1}∈A③∅∈A④{-1,1}⊆A.
①1∈A②{-1}∈A③∅∈A④{-1,1}⊆A.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |