题目内容
11.给出下列命题:(1)若f(x-1)=f(1-x),则函数f(x)的图象关于直线x=1对称;
(2)y=f(x-1)与y=f(1-x)的图象关于直线x=0对称;
(3)$y={({\frac{1}{2}})^{|x|}}-{sin^2}x+2015$无最大值也无最小值;
(4)y=$\frac{2tanx}{1-ta{n}^{2}x}$的最小正周期为π;
(5)y=sinx(0≤x≤2π)有对称轴两条,对称中心三个; 则正确命题是没有.
分析 (1)若f(x-1)=f(1-x),可得f(x)=f(-x),由函数的奇偶性即可判断出对称性;
(2)由函数y=f(x)的图象向右平移一个单位可得:y=f(x-1);由函数y=f(x)的图象关于y轴对称变换可得:y=f(-x),在向右平移一个单位可得:y=f(1-x),即可得出对称性;
(3)$y={({\frac{1}{2}})^{|x|}}-{sin^2}x+2015$=$\left\{\begin{array}{l}{(\frac{1}{2})^{x}+co{s}^{2}x+2014,x≥0}\\{{2}^{x}+co{s}^{2}x+2014,x≤0}\end{array}\right.$,即可得出最值情况;
(4)y=$\frac{2tanx}{1-ta{n}^{2}x}$=tan2x,即可得出最小正周期;
(5)y=sinx(0≤x≤2π)有对称轴两条分别为:x=$\frac{π}{2}$,x=$\frac{3π}{2}$,对称中心只有一个(π,0),即可判断出正误.
解答 解:(1)若f(x-1)=f(1-x),可得f(x)=f(-x),因此函数f(x)的图象关于y轴对称,不正确;
(2)由函数y=f(x)的图象向右平移一个单位可得:y=f(x-1);由函数y=f(x)的图象关于y轴对称变换可得:y=f(-x),在向右平移一个单位可得:y=f(1-x).因此其图象关于直线x=1对称,因此不正确;
(3)$y={({\frac{1}{2}})^{|x|}}-{sin^2}x+2015$=$\left\{\begin{array}{l}{(\frac{1}{2})^{x}+co{s}^{2}x+2014,x≥0}\\{{2}^{x}+co{s}^{2}x+2014,x≤0}\end{array}\right.$,可得最大值为2016,无最小值,因此不正确;
(4)y=$\frac{2tanx}{1-ta{n}^{2}x}$=tan2x,其最小正周期为$\frac{π}{2}$,因此不正确;
(5)y=sinx(0≤x≤2π)有对称轴两条分别为:x=$\frac{π}{2}$,x=$\frac{3π}{2}$,对称中心只有一个(π,0),因此不正确.
则正确命题是:没有.
故答案为:没有.
点评 本题考查了函数的奇偶性与对称性、函数的单调性与值域、三角函数的图象与性质、简易逻辑的判定方法、,考查了推理能力与计算能力,属于中档题.

| A. | 命题“若a>b,则a2>b2”的否命题是“若a<b,则a2<b2” | |
| B. | 命题“若a>b,则a2>b2”的逆命题是“若a≤b,则a2≤b2” | |
| C. | 命题“?x∈R,cosx<1”的否定命题是“?x0∈R,cosx0≥1” | |
| D. | 命题“?x∈R,cosx<1”的否定命题是“?x0∈R,cosx0>1” |

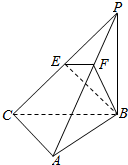 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,M为AB的中点,点F在PA上,且2PF=FA.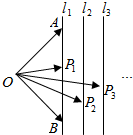 如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.
如图,已知l1,l2,l3,…ln为平面内相邻两直线距离为1的一组平行线,点O到l1的距离为2,A,B是l1的上的不同两点,点P1,P2,P3,…Pn分别在直线l1,l2,l3,…ln上.若$\overrightarrow{O{P}_{n}}$=xn$\overrightarrow{OA}$+yn$\overrightarrow{OB}$(n∈N*),则x1+x2+…+x5+y1+y2+…+y5的值为10.