题目内容
4.已知函数f(x)=$\frac{{{x^2}+3x+2a}}{x}$,x∈[2,+∞)(1)当a=$\frac{1}{2}$时,试判断f(x)在(2,+∞)上的单调性,并加以证明.
(2)若对任意x∈[2,+∞),f(x)>0恒成立,求实数a的取值范围.
分析 (1)利用函数单调性的定义,按照取值、作差、变形并判断符号、下结论的方法完成证明;
(2)这是一个不等式恒成立问题,可以转化为函数的最值问题求解,在求解之前可以先将字母a分离出来,然后构造函数,研究单调性,求其最值.
解答 解:(1)当$a=\frac{1}{2}$时,$f(x)=\frac{{x}^{2}+3x+1}{x}=x+\frac{1}{x}+3$,该函数在(2,+∞)上单调递增.
由题意设2≤x1<x2,则f(x2)-f(x1)=${x}_{2}-{x}_{1}+\frac{1}{{x}_{2}}-\frac{1}{{x}_{1}}$
=$({x}_{2}-{x}_{1})(\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}})$①
因为2≤x1<x2,所以x2-x1>0,x1x2>0,x1x2-1>0,
所以①式>0,即f(x2)-f(x1)>0,
所以f(x2)>f(x1),故函数f(x)在[2,+∞)上单调递增.
(2)由f(x)>0有$\frac{{x}^{2}+3x+2a}{x}>0$对x∈[2,+∞)恒成立,
即2a>-x2-3x对x∈[2,+∞)恒成立,
令g(x)=-x2-3x,x∈[2.+∞),
该二次函数在$(-\frac{3}{2},+∞)$上递减,所以该函数在[2,+∞)上递减,
故g(x)max=g(2)=-10.
所以要使原式成立,只需2a>g(x)max=-10成立,
即a>-5即为所求.
点评 对于函数的单调性,一般采用定义法或导数法进行判断或求解,本题用的是定义法;而不等式恒成立问题,一般转化为函数的最值解决问题,能分离参数的尽量分离参数.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
12.若直角坐标平面内两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称(P,Q)是函数y=f(x)的一个“伙伴点组”(点组(P,Q)与(Q,P)看作同一个“伙伴点组”).已知函数$f(x)=\left\{\begin{array}{l}kx-1,x>0\\-ln(-x),x<0\end{array}\right.$,有两个“伙伴点组”,则实数k的取值范围是( )
| A. | (-∞,0) | B. | (0,1) | C. | (0,$\frac{1}{2}$) | D. | (0,+∞) |
13.已知矩形ABCD,PA⊥面ABCD,连接AC、BD、PB、PC、PD,则下列各组向量中数量积不为0的是( )
| A. | $\overrightarrow{PC}$和$\overrightarrow{BD}$ | B. | $\overrightarrow{DA}$和$\overrightarrow{PB}$ | C. | $\overrightarrow{PD}$与$\overrightarrow{AB}$ | D. | $\overrightarrow{PC}$与$\overrightarrow{AD}$ |
14.设x∈R,则“x<1”是“x|x|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
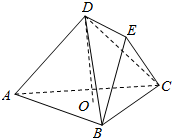 如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.
如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.