题目内容
函数f(x)=3x2+2(a-1)x-3在(-∞,1]上递减,则a的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据二次函数的性质,得出-
≥1,即可求解.
| a-1 |
| 3 |
解答:
解:∵函数f(x)=3x2+2(a-1)x-3在(-∞,1]上递减,
∴-
≥1,
即a≤-2
故答案为:(-∞,-2]
∴-
| a-1 |
| 3 |
即a≤-2
故答案为:(-∞,-2]
点评:本题考查了二次函数的性质,解不等式,属于基础题,难度较小.

练习册系列答案
相关题目
已知命题p:若2b=a+c,则a、b、c成等差数列;命题q:若b2=ac,则a、b、c成等比数列,则下列命题中是真命题的是( )
| A、¬p或q | B、p且q |
| C、¬p且¬q | D、¬p或¬q |
已知log2[log2(log2x)]=0,则x
=( )
| 1 |
| 2 |
A、
| ||
| B、2 | ||
C、2
| ||
D、4
|
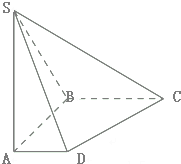 如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=