题目内容
设等差数列{an}的前n项和为Sn.且S4=4S2,a2n=2an+1.
(1)求数列{an}的通项公式;
(2)数列{bn}满足:b1=3,bn-bn-1=an+1(n≥2),求数列{
}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)数列{bn}满足:b1=3,bn-bn-1=an+1(n≥2),求数列{
| 1 |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)设等差数列的首项为a1,公差为d,由题意构造方程组,解得即可,从而可求出数列的通项公式;
(2)利用叠加法求出数列{bn}的通项公式,然后利用裂项法进行求和即可.
(2)利用叠加法求出数列{bn}的通项公式,然后利用裂项法进行求和即可.
解答:
解:(1)设等差数列的首项为a1,公差为d,则4a1+
d=4(2a1+d),a1+(2n-1)d=2a1+2(n-1)d+1,解得a1=1,d=2
∴an=2n-1.
(2)数列{bn}满足:b1=3,bn-bn-1=an+1,
∴bn-bn-1=2n+1
∴b2-b1=2×2+1,
b3-b2=2×3+1,
…
bn-bn-1=2n+1,
累加可得,
∴bn-b1=2(2+3+4+…+n)+n-1=n2+n-2+n-1,
∴bn=n2+2n=n(n+2),
验证当n=1时,b1=1+2=3,成立
∴
=
(
-
)
∴Tn=
+
+…+
=
[(1-
)+(
-
)+…(
-
)+(
-
)]
=
(1+
-
-
)
=
-
| 4×3 |
| 2 |
∴an=2n-1.
(2)数列{bn}满足:b1=3,bn-bn-1=an+1,
∴bn-bn-1=2n+1
∴b2-b1=2×2+1,
b3-b2=2×3+1,
…
bn-bn-1=2n+1,
累加可得,
∴bn-b1=2(2+3+4+…+n)+n-1=n2+n-2+n-1,
∴bn=n2+2n=n(n+2),
验证当n=1时,b1=1+2=3,成立
∴
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Tn=
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 3 |
| 4 |
| 2n+3 |
| 2n2+6n+4 |
点评:本题主要考查了利用递推关系求数列的通项公式,以及利用叠加法裂项求数列的和,同时考查了计算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
对任意x,y满足f(x+y2)=f(x)+2[f(y)]2,且f(1)≠0,则f(2013)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:若2b=a+c,则a、b、c成等差数列;命题q:若b2=ac,则a、b、c成等比数列,则下列命题中是真命题的是( )
| A、¬p或q | B、p且q |
| C、¬p且¬q | D、¬p或¬q |
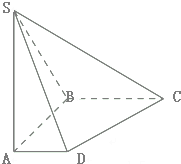 如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
如图,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=