题目内容
已知集合A={0,1},B={x|x2-2ax+a2-
=0}
(1)若A∪B=B,求实数a所满足的条件;
(2)若A∩B=B,求实数a的取值范围.
| a |
| 2 |
(1)若A∪B=B,求实数a所满足的条件;
(2)若A∩B=B,求实数a的取值范围.
考点:交集及其运算,并集及其运算
专题:集合
分析:(1)由A与B的并集为B,得到A为B的子集,把x=0与x=1代入求出a的值即可;
(2)由A与B的交集为B,得到B为A的子集,求出a的范围即可.
(2)由A与B的交集为B,得到B为A的子集,求出a的范围即可.
解答:
解:(1)∵A∪B=B,∴A⊆B,
∴x=0和x=1为x2-2ax+a2-
=0的解,
即0+1=2a,且a2-
=0,
解得:a=
;
(2)∵A∩B=B,∴B⊆A,
∴当B=∅时,则有△<0,即4a2-4(a2-
)=2a<0,
解得:a<0;
当B≠∅时,x=0或x=1是方程x2-2ax+a2-
=0的解,
把x=0代入方程得:a2-
=0,
解得:a=0或a=
;
把x=1代入方程得:1-2a+a2-
=0,
解得:a=
或a=2,
综上,a的范围为{a|a≤0或a=
或a=2}.
∴x=0和x=1为x2-2ax+a2-
| a |
| 2 |
即0+1=2a,且a2-
| a |
| 2 |
解得:a=
| 1 |
| 2 |
(2)∵A∩B=B,∴B⊆A,
∴当B=∅时,则有△<0,即4a2-4(a2-
| a |
| 2 |
解得:a<0;
当B≠∅时,x=0或x=1是方程x2-2ax+a2-
| a |
| 2 |
把x=0代入方程得:a2-
| a |
| 2 |
解得:a=0或a=
| 1 |
| 2 |
把x=1代入方程得:1-2a+a2-
| a |
| 2 |
解得:a=
| 1 |
| 2 |
综上,a的范围为{a|a≤0或a=
| 1 |
| 2 |
点评:此题考查了交集及其运算,以及并集及其运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
已知复数z的共轭复数是
,则复数z2+
+3等于( )
| 2-2i |
| 1+i |
. |
| z |
| A、-2i | B、3-i |
| C、1+2i | D、-1-2i |
设a,b,c∈(0,+∞),则三个数a+
,b+
,c+
的值( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、都大于2 |
| B、都小于2 |
| C、至少有一个不大于2 |
| D、至少有一个不小于2 |
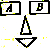 用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )
用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )