题目内容
若x0是函数f（x）=2x-x-3的零点，则[x0]（表示不超过x0的最大整数）的值为 ．
考点：函数的零点
专题：函数的性质及应用
分析：可以看作y=2x与g（x）=3+x交点问题，画出图象判断，利用零点存在性定理，f（-3）•f（-2）=
×（
-1）＜0，f（2）•f（3）=（-1）（2）=-2＜0，
得出x0∈（-3，-2）或x0∈（2，3），在判断即可．
| 1 |
| 8 |
| 1 |
| 4 |
得出x0∈（-3，-2）或x0∈（2，3），在判断即可．
解答：
解：∵函数f（x）=2x-x-3的零点，
∴可以看作y=2x与g（x）=3+x交点问题．
画出图象判断，利用零点存在性定理
∵f（-3）•f（-2）=
×（
-1）＜0，f（2）•f（3）=（-1）（2）=-2＜0，
∴x0∈（-3，-2）或x0∈（2，3），
∴[x0]的值为-3或2，
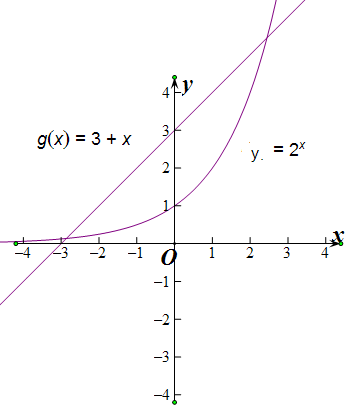
故答案为；-3或2
∴可以看作y=2x与g（x）=3+x交点问题．
画出图象判断，利用零点存在性定理
∵f（-3）•f（-2）=
| 1 |
| 8 |
| 1 |
| 4 |
∴x0∈（-3，-2）或x0∈（2，3），
∴[x0]的值为-3或2，
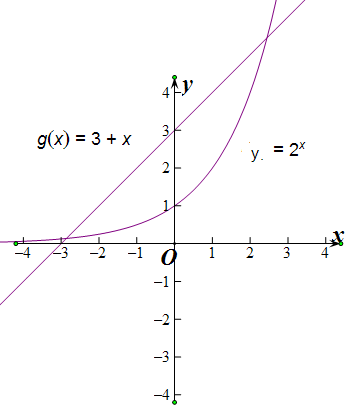
故答案为；-3或2
点评：本题考查了函数的图象的运用，零点的存在性定理，属于中档题，关键是估计区间．
练习册系列答案
相关题目
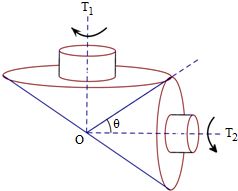如图所示，某传动装置由两个陀螺T1，T2组成，陀螺之间没有滑动．每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成，每个圆柱的底面半径和高都是相应圆锥底面半径的在同一坐标系中，函数y=3x的图与y=(
)x的图象（ ）
| 1 |
| 3 |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |