题目内容
设点M、N分别是不等边△ABC的重心与外心,已知A(0,1),B(0,-1),且
=λ
.
(1)求动点C的轨迹E;
(2)(理科)若直线y=kx+b与曲线E交于不同的两点P、Q,且满足
•
=0,求实数b的取值范围.
(文科)若直线y=x+b与曲线E交于不同的两点P、Q,且满足
•
=0,求实数b的取值.
| MN |
| AB |
(1)求动点C的轨迹E;
(2)(理科)若直线y=kx+b与曲线E交于不同的两点P、Q,且满足
| OP |
| OQ |
(文科)若直线y=x+b与曲线E交于不同的两点P、Q,且满足
| OP |
| OQ |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)设点C(x,y ),运用重心坐标公式可得点M,由
=λ
,可得 MN∥AB,故N的横坐标等于
,又N在AB的中垂线上,故纵坐标等于0.由于NA=NC,可得方程,化简可得轨迹方程,从而得到轨迹.
(2)(理科)把直线y=kx+b代入轨迹E的方程化简,再由韦达定理,结合向量数量积为0,化简整理,即可得到b的取值范围;
(文科)把直线y=x+b代入轨迹E的方程化简,再由韦达定理和判别式大于0,结合向量数量积为0,化简整理,即可得到b的取值.
| MN |
| AB |
| x |
| 3 |
(2)(理科)把直线y=kx+b代入轨迹E的方程化简,再由韦达定理,结合向量数量积为0,化简整理,即可得到b的取值范围;
(文科)把直线y=x+b代入轨迹E的方程化简,再由韦达定理和判别式大于0,结合向量数量积为0,化简整理,即可得到b的取值.
解答:
解:(1)设点C(x,y ),则点M(
,
),
即点M(
,
),
由
=λ
,可得 MN∥AB,故N的横坐标等于
,
又N在AB的中垂线上,故纵坐标等于0.
由于N是不等边△ABC的外心,∴NA=NC,
∴
=
.
化简可得,
+y2=1,xy≠0,
故动点C的轨迹E是焦点在x轴上的标准位置的一个椭圆,去掉其顶点.
(2)(理科)将直线y=kx+b代入方程
+y2=1(xy≠0),化简可得,
(1+3k2)x2+6kbx+3b2-3=0,由题意可得,
b≠0,b≠±1且△=(6kb)2-4(1+3k2)(3b2-3)>0,
化简得,b≠0,b≠±1且b2-1<3k2,
设P(x1,y1),Q(x2,y2),
由
•
=0,可得,
x1•x2+(kx1+b)•(kx2+b)=(1+k2)x1•x2+kb(x1+x2)+b2=0.
x1+x2=-
,x1x2=
,
即有(1+k2)•
+kb•(-
)+b2=0
解得,3k2=4b2-3,
则b≠0,b≠±1,4b2-3≥0,4b2-3>b2-1,
解得,b≤-
或b≥
且b≠±1.
(文科)把直线y=x+b代入轨迹E的方程化简可得 4x2+6bx+3b2-3=0.
由题意可得,b≠0,b≠±1,
且△=36b2-16( 3b2-3)>0,解得,b≠0,b≠±1且b2<4,
x1+x2=-
,x1•x2=
.
由
•
=0,可得,
x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0.
∴2•
+b•(
)+b2=0,解得 b2=
,
∴b=±
.
| 0+0+x |
| 3 |
| 1-1+y |
| 3 |
即点M(
| x |
| 3 |
| y |
| 3 |
由
| MN |
| AB |
| x |
| 3 |
又N在AB的中垂线上,故纵坐标等于0.
由于N是不等边△ABC的外心,∴NA=NC,
∴
(
|
(
|
化简可得,
| x2 |
| 3 |
故动点C的轨迹E是焦点在x轴上的标准位置的一个椭圆,去掉其顶点.
(2)(理科)将直线y=kx+b代入方程
| x2 |
| 3 |
(1+3k2)x2+6kbx+3b2-3=0,由题意可得,
b≠0,b≠±1且△=(6kb)2-4(1+3k2)(3b2-3)>0,
化简得,b≠0,b≠±1且b2-1<3k2,
设P(x1,y1),Q(x2,y2),
由
| OP |
| OQ |
x1•x2+(kx1+b)•(kx2+b)=(1+k2)x1•x2+kb(x1+x2)+b2=0.
x1+x2=-
| 6kb |
| 1+3k2 |
| 3b2-3 |
| 1+3k2 |
即有(1+k2)•
| 3b2-3 |
| 1+3k2 |
| 6kb |
| 1+3k2 |
解得,3k2=4b2-3,
则b≠0,b≠±1,4b2-3≥0,4b2-3>b2-1,
解得,b≤-
| ||
| 2 |
| ||
| 2 |
(文科)把直线y=x+b代入轨迹E的方程化简可得 4x2+6bx+3b2-3=0.
由题意可得,b≠0,b≠±1,
且△=36b2-16( 3b2-3)>0,解得,b≠0,b≠±1且b2<4,
x1+x2=-
| 3b |
| 2 |
| 3b2-3 |
| 4 |
由
| OP |
| OQ |
x1•x2+(x1+b)•(x2+b)=2x1•x2+b(x1+x2)+b2=0.
∴2•
| 3b2-3 |
| 4 |
| -3b |
| 2 |
| 3 |
| 2 |
∴b=±
| ||
| 2 |
点评:本题考查点的轨迹方程的求法,直线和圆锥曲线的位置关系,判断轨迹E的形状,是解题的易错点.

练习册系列答案
相关题目
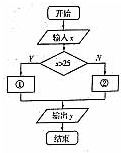 某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )
某客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过25kg按0.5元/kg收费,超过25kg的部分按0.8元/kg收费,计算收费的程序框图如右图所示,则①②处应填( )| A、y=0.8x y=0.5x |
| B、y=0.5x y=0.8x |
| C、y=25×0.5+(x-25)×0.8 y=0.5x |
| D、y=25×0.5+0.8x y=0.8x |
在边长为a的正方形内随机取一个点,则此点落在该正方形的内切圆内部的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合M={x|x<2012},N={x|0<x≤2012},则M∪N=( )
| A、M |
| B、N |
| C、{x|x≤2012} |
| D、{x|0<x<2012} |
已知数列{an}的前n项和为Sn,且Sn=2an-1(n∈N*),则a4=( )
| A、8 | B、16 | C、31 | D、32 |
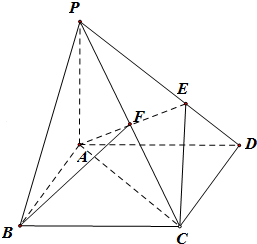 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中点,